머신러닝/딥러닝 공부
신경망 (2) - 다층 퍼셉트론(Multi Layer Perceptron)과 활성화 함수(Activation function) 본문
신경망 (2) - 다층 퍼셉트론(Multi Layer Perceptron)과 활성화 함수(Activation function)
호사린가마데라닌 2021. 11. 22. 23:35
1) 다층 퍼셉트론 (multi layer perceptron)
단층 퍼셉트론(single layer perceptron)에 관한 내용은 아래의 포스팅에서 볼 수 있습니다.
https://yhyun225.tistory.com/20
신경망 (1) - 단층 퍼셉트론 (Single Layer Perceptron)
퍼셉트론(perceptron)에 대해서는 이미 앞의 포스팅에서 다루었습니다. 한 가지 짚고 넘어갈 점은 퍼셉트론은 선형 방정식을 통해 값을 계산하는 알고리즘이라는 것입니다. https://yhyun225.tistory.com/12
yhyun225.tistory.com
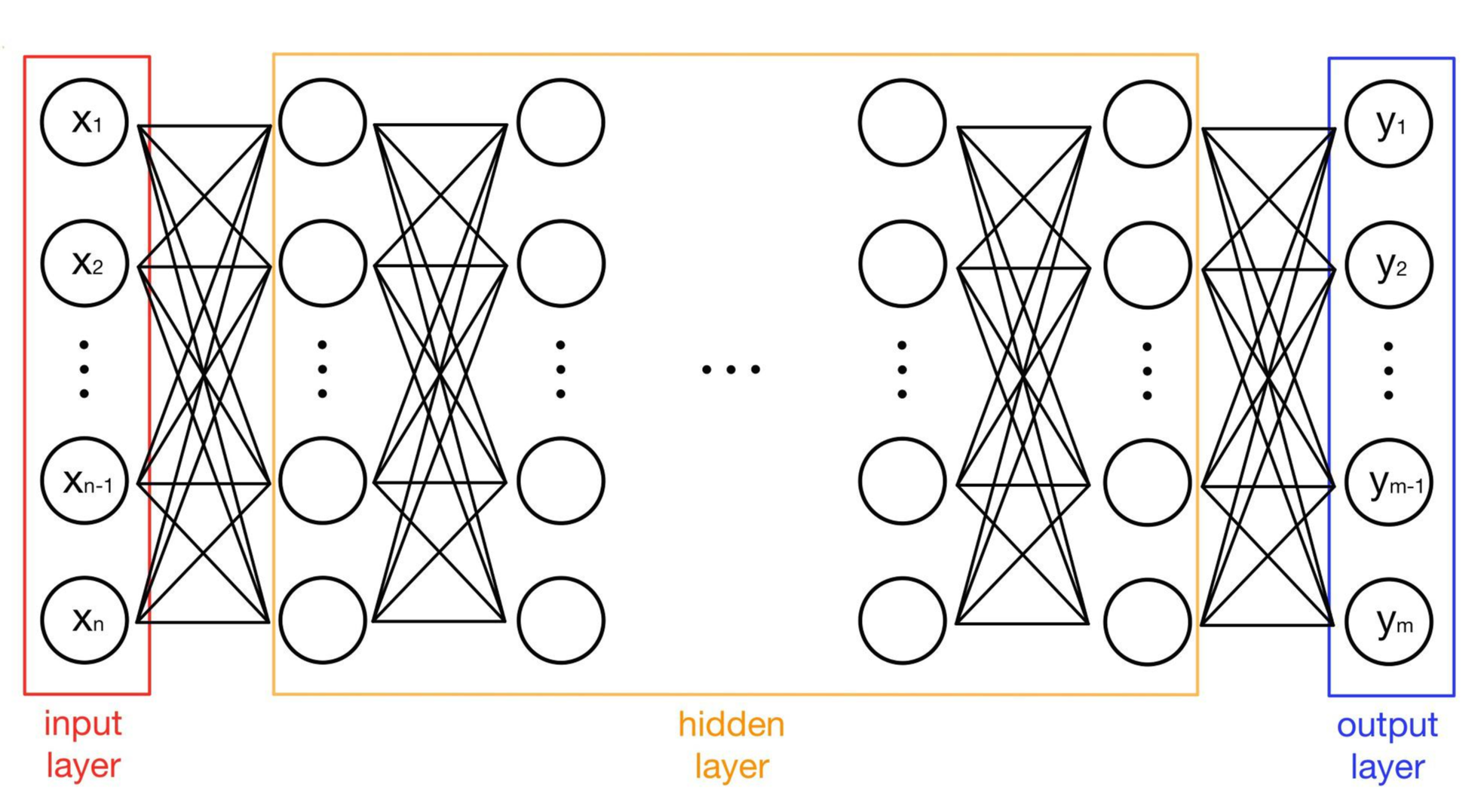
다층 퍼셉트론(multi layer perceptron)은 층이 2개 이상 존재하는 신경망입니다. 입력층(input layer)과 출력층(output layer)을 제외한 층을 은닉층(hidden layer)이라고 합니다. 이때 은닉층이 1개만 있는 다층 퍼셉트론의 경우 얕은 신경망(shallow neural network), 은닉층이 2개 이상인 경우 깊은 신경망(deep neural network)라고 합니다. 그리고 이 깊은 신경망을 학습시키는 것을 딥러닝(deep learning)이라고 합니다.
다층 퍼셉트론은 단층 퍼셉트론과 달리 비선형으로 분포하는 데이터들에 대해 학습이 가능합니다. 다층 퍼셉트론은 가중치에 대해 선형 방정식을 계산하기 때문에 층과 층 사이에서 선형으로 표현된 데이터를 비선형으로 바꿔주는 과정이 필요합니다. 이 과정을 담당하는 것이 바로 활성화 함수(activation function)입니다.
2) 활성화 함수(activation function)
다층 퍼셉트론은 하나의 층에서 다른 층으로 값을 넘길 때 선형 방정식을 이용하여 값을 계산한 뒤 넘깁니다. 그런데 선형으로 표현된 데이터들은 아무리 층을 통과하여도 선형이라는 성질을 잃지 않습니다.
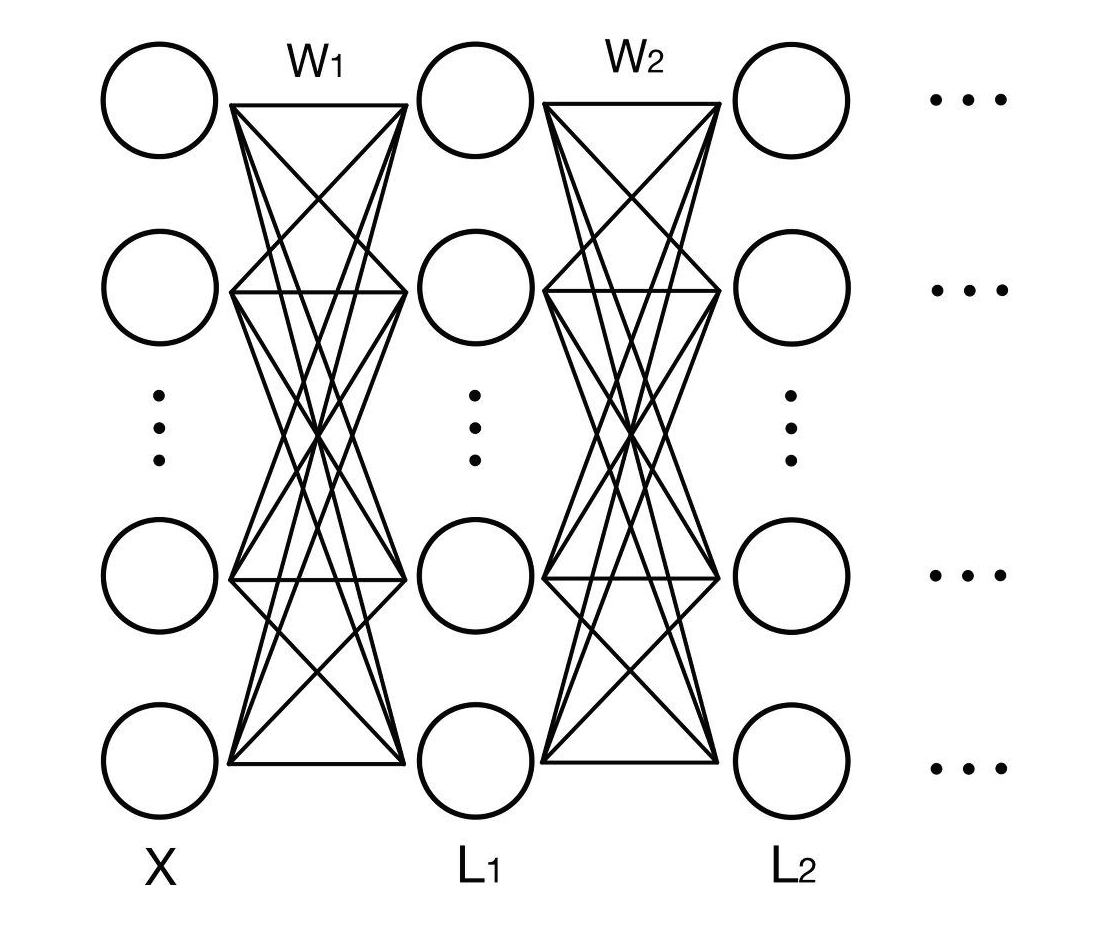
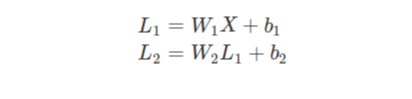
위의 수식의 L1과 L2는 각각 첫 번째 은닉층을 통과한 데이터와 두 번째 은닉층을 통과한 데이터입니다. 하지만 아래의 수식으로 확인할 수 있듯이 결국 층을 몇 번 통과하여도 선형이라는 성질은 사라지지 않습니다.

따라서 층과 층 사이를 통과할때 선형 데이터를 비선형으로 바꿔주기 위해서 활성화 함수를 사용합니다. 로지스틱 회귀에서 사용했던 sigmoid함수와 다중 분류에서 사용했던 softmax함수도 활성화 함수입니다.
활성화 함수는 여러 종류가 있습니다. 종류 별로 살펴보겠습니다.
밑의 그래프에서 파란선은 활성화 함수를, 빨간 점선은 활성화 함수의 도함수를 나타낸 그래프입니다.
가장 유명한(제가 자주 접한) 활성화 함수들을 우선적으로 정리하겠습니다.
-sigmoid함수
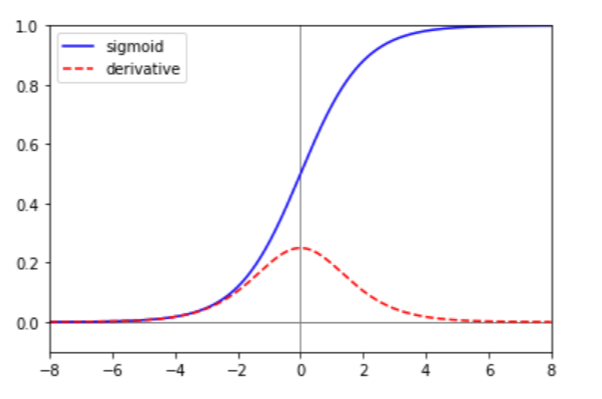

sigmoid 함수는 입력으로 받은 값을 0과 1 사이의 값으로 바꿔줍니다. 이 때문에 결괏값을 확률처럼 해석하는 로지스틱 회귀 등의 모델에 적합한 활성화 함수입니다.
sigmoid 함수는 입력으로 받은 값의 절댓값이 크면 기울기가 0으로 수렴하는 것을 관찰할 수 있습니다. 따라서 경사 하강법을 적용하여 가중치를 업데이트할 때 기울기가 0에 가까워져 소실되는 기울기 소실(Gradient Vanishing) 현상이 발생할 수 있습니다. 또한 미분값의 최댓값이 0.25로 상당히 작은 수치인데, 층이 깊어질수록 곱해지는 미분 값이 누적되어 가중치의 업데이트량이 점점 더 작아져 가중치를 제대로 업데이트할 수 없다는 단점 때문에 딥러닝에서는 잘 사용하지 않는 활성화 함수입니다.
- tanh(hyperbolic tangent)함수
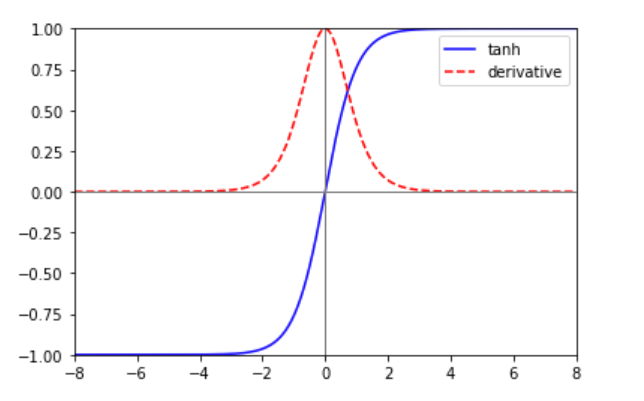

tanh함수는 simgoid함수를 변형한 함수입니다. 함수의 중심이 원점으로 옮겨가 경사 하강법을 이용하여 가중치를 최적화할 때 sigmoid함수보다 원활하게 작동하지만 함수의 형태는 sigmoid와 같기 때문에 여전히 vanishing gradient문제를 가지고 있습니다.
- ReLU(Rectified Linear Unit) 함수
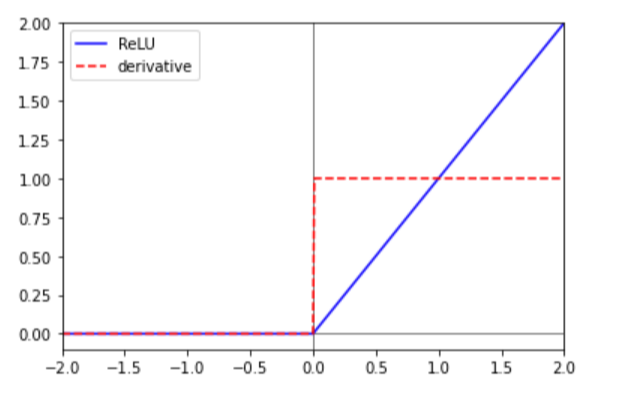
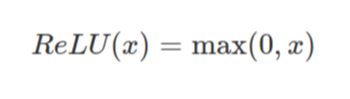
ReLu함수는 0보다 큰 입력값의 경우 그대로 출력하며 0 이하의 값은 다음 층에 전달하지 않습니다. 이 함수는 sigmoid함수와 tanh함수가 가지고 있는 vanishing gradient문제를 완화해주기 때문에 CNN(Convolution Neural Network)에서 자주 쓰입니다.
0보다 큰 입력값은 그대로, 0 이하의 값은 0으로 만들어버리기 때문에 0 이하의 값들은 다음 층(layer)으로 전달되지 않습니다. 이를 dying ReLU현상이라 합니다. 이 현상을 해결하기 위해 0보다 작은 경우 약간의 변화량만이라도 다음 층으로 전달할 수 있도록 해주는 Leaky ReLU와 PReLU가 만들어지기도 했습니다.
- ELU(Exponential Linear Unit) 함수
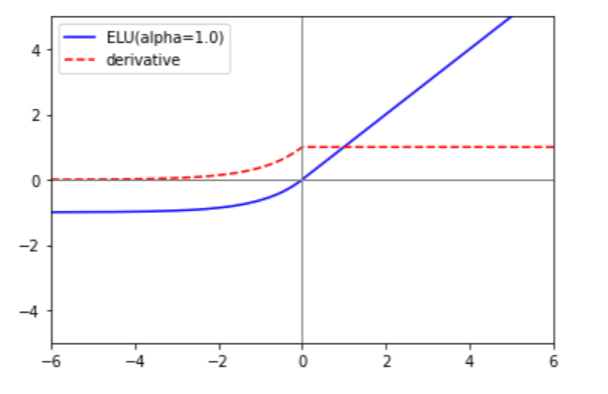


ELU함수는 ReLU의 장점을 모두 가지며 dying ReLU현상을 해결한 함수입니다. 파라미터를 이용하여 입력값이 0 이하일 때의 지수함수 부분의 scale을 조절할 수 있으며, 알파가 1인 경우 위의 왼쪽 그래프와 같이 연속인 도함수를 갖습니다. 알파가 1 이외의 경우 SeLU(Scaled exponential Linear Unit)이라고 부르며 불연속인 도함수를 갖습니다.
ReLU함수와 달리 지수함수의 계산이 들어가므로 ReLU를 사용할 때보다 연산량이 증가합니다.
-softplus함수


softplus함수는 ReLU함수를 부드럽게 근사 시킨 함수입니다. 전구간에서 미분이 가능한 함수이며, 도함수가 sigmoid함수가 되기 때문에 기울기가 0~1 사이의 값을 갖습니다.
이 밖에도 정말 많은 활성화 함수가 존재합니다. 다음에 기회가 된다면 다른 활성화 함수도 정리해 보도록 하겠습니다.
활성화 함수의 역할은 모델의 층과 층 사이에서 데이터가 이동할 때 선형성을 잃도록 데이터를 처리해주는 것입니다. 만일 활성화 함수로 선형 함수를 사용한다면 결국 층을 깊게 쌓아봤자 하나의 층으로 표현이 가능해집니다. 따라서 활성화 함수는 항상 비선형 함수를 채택하여 사용해야 합니다.
다음 포스팅에서는 깊은 신경망에서 가중치와 바이어스를 업데이트시키는 알고리즘인 역전파 알고리즘(back-propagation algorithm)에 대해 정리해보도록 하겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 분류 (6) - 다층 퍼셉트론 코드 (파이썬 구현) (0) | 2021.12.02 |
|---|---|
| 신경망 (3) - 역전파 알고리즘(BackPropagation algorithm) (1) | 2021.11.25 |
| 신경망 (1) - 단층 퍼셉트론 (Single Layer Perceptron) (0) | 2021.11.21 |
| 분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 ) (0) | 2021.11.18 |
| 데이터 세트 (3) - 규제(Regularization), 라쏘 회귀(Lasso Regression)와 릿지 회귀(Ridge Regression) (0) | 2021.11.17 |




