분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 )

 

1) 다중 분류 모델 코드

이전 포스팅에서 수정했던 다중 분류 코드를 가져오겠습니다.
https://yhyun225.tistory.com/15?category=964332

분류 (4) - 다중 분류 (Multiclass Classification) 코드 구현

이 다중 분류 클래스에 predict(), score(), val_loss() 함수를 추가하겠습니다. 각 함수에 대한 설명은 아래 포스팅에 있습니다.
https://yhyun225.tistory.com/16

데이터 세트(1) - 훈련 세트(training set), 테스트 세트(test set), 검증 세트(validation set)

완성된 다중 분류 모델의 코드는 다음과 같습니다.

class Multiclass:
  def __init__(self,learning_rate=0.01):
    self.w=None #가중치 행렬
    self.b=None #바이어스 배열
    self.lr=learning_rate #학습률 
    self.val_losses=[] #매 에포크마다 검증세트 손실을 저장할 리스트
    self.losses=[] #매 에포크마다 손실 저장할 리스트
    self.weight_history=[] #매 에포크마다 가중치 저장할 리스트
    self.bias_history=[] #매 에포크마다 바이어스 저장할 리스트

  def forward(self,x):
    z=np.dot(x,self.w)+self.b
    z=np.clip(z,-100,None) #NaN 방지
    return z

  def softmax(self,z):
    exp_z=np.exp(z)
    a=exp_z/np.sum(exp_z)
    return a

  def loss(self,x,y):
    z=self.forward(x)
    a=self.softmax(z)
    return -np.sum(y*np.log(a)) #손실 계산 후 리턴

  def gradient(self,x,y):
    z=self.forward(x) #선형방정식을 통한 z값 산출
    a=self.softmax(z) #z값을 softmax에 통과시켜 a값 산출

    w_grad=-np.dot(x.reshape(-1,1),(y-a).reshape(1,-1)) #가중치의 기울기
    b_grad=-(y-a) #바이어스의 기울기

    return w_grad,b_grad

  def fit(self,x_data,y_data,epochs=10,x_val=None,y_val=None):
    #가중치와 바이어스 초기화
    self.w=np.random.normal(0,1,(x_data.shape[1],y_data.shape[1])) #표준정규분포로 초기화 
    self.b=np.zeros(y_data.shape[1]) #0으로 초기화

    #에포크
    for epoch in range(epochs):
      l=0 #손실값을 계산할 변수
      w_grad=np.zeros((x_data.shape[1],y_data.shape[1])) #손실함수에 대한 가중치의 기울기
      b_grad=0 #손실함수에 대한 바이어스의 기울기

      for x,y in zip(x_data,y_data):
        l+=self.loss(x,y) #매 에포크마다 손실값 계산

        w_i,b_i=self.gradient(x,y) #가중치와 바이어스의 기울기를 계산

        w_grad+=w_i #가중치의 기울기 누적
        b_grad+=b_i #바이어스의 기울기 누적 

      self.w-=self.lr*(w_grad/len(y_data)) #가중치 업데이트
      self.b-=self.lr*(b_grad/len(y_data)) #바이어스 업데이트

      val_loss=self.val_loss(x_val,y_val)

      self.val_losses.append(val_loss)
      self.losses.append(l/len(y_data)) #손실 저장
      self.weight_history.append(self.w) #가중치 저장
      self.bias_history.append(self.b) #바이어스 저장

      print(f'epoch({epoch+1}) ===> loss : {l/len(y_data):.5f} | val_loss : {val_loss:.5f}')


  def predict(self,x_data):
    z=self.forward(x_data)
    return np.argmax(z,axis=1) #가장 큰 인덱스 리턴

  def score(self,x_data,y_data):
    return np.mean(self.predict(x_data)==np.argmax(y_data,axis=1))

  def val_loss(self,x_val,y_val):
    val_loss=0
    for x,y in zip(x_val,y_val):
      val_loss+=self.loss(x,y)

    return val_loss/len(y_val)

전반적인 코드는 기존의 코드와 비슷하지만, fit() 메소드가 인자로 x_val과 y_val을 받는 점이 다릅니다. 검증 세트에 대한 손실을 측정하기 위해 위와 같은 인자를 추가했습니다. 또한 매 에포크마다 검증 손실을 저장하기 위해 self.val_losses라는 리스트를 선언하였습니다.

2) MNIST 숫자 손글씨 데이터 세트 전처리

mnist 숫자 손글씨 데이터 세트

MNIST 숫자 손글씨 데이터 세트는 사람이 손으로 적은 숫자들에 대한 데이터 세트입니다. 훈련 세트(training set)와 테스트 세트(test set)로 나누어져 있으며 각각 60000개, 10000개의 숫자 이미지를 가지고 있습니다.


각 이미지는 28필셀 x 28픽셀(총 784 픽셀)의 크기를 가지고 있으며, 흑백 사진입니다. 각 픽셀은 0~255의 값을 가지고 있으며 값이 0에 가까울수록 검은색에 가깝고, 값이 255에 가까울수록 흰색에 가깝습니다.


훈련 데이터는 28 x 28 의 2차원 배열에 각 위치의 픽셀 값이 저장되어 있는 형태입니다. 타깃은 각 이미지가 0부터 9까지 어떤 숫자를 나타내는지 숫자 값을 가지고 있습니다.


이제 MNIST 숫자 손글씨 데이터 세트를 받아오겠습니다. MNIST 숫자 손글씨 데이터 세트는 tensorflow의 keras.datasets.mnist 모듈 아래 load_data()를 이용하여 불러올 수 있습니다. 이때 load_data()는 훈련 세트(training set)와 테스트 세트(test set) 각각의 데이터와 타깃을 튜플 형태로 반환하기 때문에 아래 코드와 같이 튜플을 이용하여 받아주었습니다.

from tensorflow import keras 
(x_train,y_train),(x_test,y_test)=keras.datasets.mnist.load_data()

각각의 shape를 살펴보겠습니다.

print('<training set>') 
print(f'x_train : {x_train.shape} y_train : {y_train.shape}') 
print() 
print('<test set>') 
print(f'x_train : {x_test.shape} y_train : {y_test.shape}') 
print()

훈련 세트의 데이터는 28 x 28 배열이 60000개, 타깃 또한 60000개, 테스트 세트 또한 각각 10000개, 10000개씩 있는 것을 확인할 수 있습니다.


다음 코드를 이용하여 데이터가 어떤 모습을 하고 있는지 확인할 수 있습니다.

import matplotlib.pyplot as plt 
plt.imshow(x_train[10],cmap='gray') 
plt.show()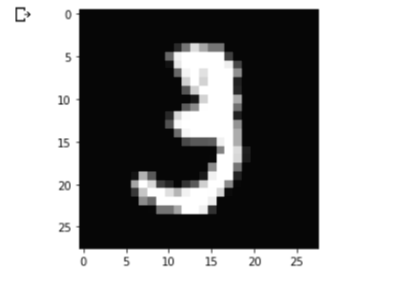

x_train 리스트의 11번째 데이터는 숫자 3에 대한 손글씨의 픽셀값을 담고 있는 2차원 배열입니다.


훈련 세트를 4:1 비율로 훈련 세트와 검증 세트로 나누어주겠습니다. sklearn의 train_test_split함수를 사용하였습니다.

from sklearn.model_selection import train_test_split 
x_train,x_val,y_train,y_val=train_test_split(x_train,y_train,stratify=y_train,test_size=0.2)

각 세트의 shape를 살펴보면 다음과 같습니다.

print('<training set>') 
print(f'x_train : {x_train.shape} y_train : {y_train.shape}') 
print() print('<validation set>') 
print(f'x_train : {x_val.shape} y_val : {y_val.shape}') 
print() print('<test set>') 
print(f'x_test : {x_test.shape} y_test : {y_test.shape}')

원하는 비율대로 잘 나누어진 것 같습니다.


모델을 학습시키기 전에 신경써야할 점이 있습니다. 위에서 만든 다중 분류 모델은 1차원 배열의 입력값과 1차원 배열의 레이블(분류 모델에서는 타깃 대신 레이블(label)이라는 용어를 자주 사용합니다)이 필요합니다.


따라서 28 x 28 크기의 2차원 배열들은 1 x 784 크기의 배열로 바꿔 주어야 합니다. 배열 내 값들은 0~255까지의 값을 가지고 있었습니다. 이를 0~1 사이의 값으로 바꿔주기 위해 255로 나누어주었습니다. 이는 훈련 데이터를 표준화(Standardization)하여 수렴 안정성을 높이는 효과를 모방하기 위해서입니다. 엄밀히 말해 255로 나누는 것이 정확한 표준화는 아니지만, 대체로 좋은 성능을 보이므로 자주 사용하는 방법입니다.


값으로 존재하는 레이블들은 one-hot encoding을 이용하여 1 x 10의 배열로 만들어줍니다. keras.utils모듈의 to_categorical() 함수를 이용하면 one-hot encoding을 쉽게 구현할 수 있습니다.

# 28 x 28 배열을 1 x 784 배열로 바꿈 
x_train = x_train.reshape(x_train.shape[0],28*28) 
x_val=x_val.reshape(x_val.shape[0],28*28) 
x_test = x_test.reshape(x_test.shape[0],28*28) 

# 0~255 값 분포를 0~1 사이에 분포하도록 바꿈 
x_train = x_train.astype('float32') / 255. 
x_val=x_val.astype('float32')/255. 
x_test = x_test.astype('float32') / 255. 

# one-hot encoding 
y_train = keras.utils.to_categorical(y_train, 10) 
y_val=keras.utils.to_categorical(y_val,10) 
y_test = keras.utils.to_categorical(y_test, 10)

바뀐 각 세트에 대한 shape를 보면 다음과 같습니다.

이제 모델을 학습시킬 준비가 끝났습니다.

3) 다중 분류 모델 학습

 

model=Multiclass(learning_rate=1.0) 
model.fit(x_train,y_train,epochs=50,x_val=x_val,y_val=y_val)

다중 분류 모델을 생성하고 학습을 시켜 보겠습니다. 학습률은 1.0으로 주었고 50에포크 동안 학습을 진행하였습니다. 또한 검증 손실을 확인하기 위해 위에서 만들었던 검증 세트 x_val, y_val를 인자로 주었습니다. 훈련 세트가 꽤 크기 때문에 시간이 조금 소요됩니다. 결과는 다음과 같습니다.

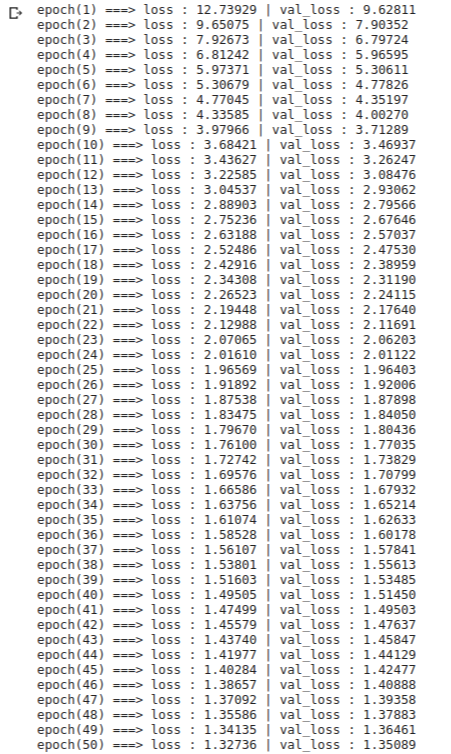
학습된 모델의 학습곡선을 그려보겠습니다.

import matplotlib.pyplot as plt 
plt.plot(model.losses,label='loss') 
plt.plot(model.val_losses,label='val_loss') 
plt.xlabel('epoch') plt.ylabel('loss') 
plt.legend() 
plt.plot()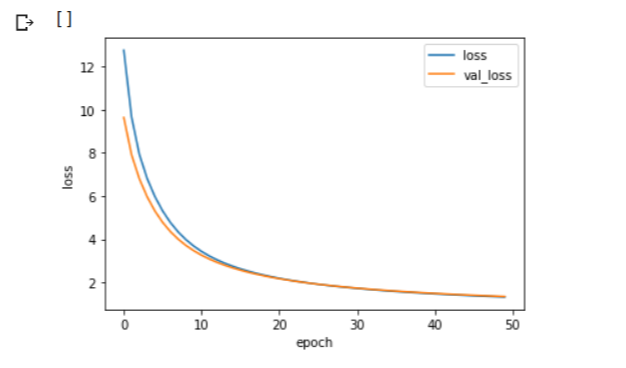

훈련 손실과 검증 손실이 초반에는 빠르게 감소하다가 점점 천천히 어떤 값에 수렴하는 것을 볼 수 있습니다. 경사하강법을 적용했기에 나타나는 현상입니다.


이 모델의 성능을 평가해보겠습니다.

model.score(x_test,y_test)

 

이 모델은 약 75%의 정확도를 보이고 있네요. 에포크를 더 크게 주어 더 오래 학습을 시키면 모델의 정확도가 올라가긴 합니다(100에포크에서 약 84%의 정확도를 보였습니다). 하지만 이는 실전에서 사용하기에 좋은 정확도라고 할 수 없습니다. 이러한 이미지 데이터에 대하여 아주 높은 정확도를 보이는 모델이 존재합니다. 바로 합성곱 신경망(Convolutional Neural Network, CNN)입니다. 이에 대해서는 딥러닝에 대해 정리할 때 다루도록 하겠습니다.