머신러닝/딥러닝 공부
데이터 세트 (3) - 규제(Regularization), 라쏘 회귀(Lasso Regression)와 릿지 회귀(Ridge Regression) 본문
데이터 세트 (3) - 규제(Regularization), 라쏘 회귀(Lasso Regression)와 릿지 회귀(Ridge Regression)
호사린가마데라닌 2021. 11. 17. 17:09
1) 규제(Regularization)
규제(Regularization)는 모델이 과대 적합을 피하여 일반화 성능을 잃지 않도록 가중치를 제한하는 방법으로, 과대 적합을 완화하기 위한 대표적인 방법입니다.
규제는 손실함수에 가중치의 노름(norm)을 더한 함수를 목적 함수(Objective function)로 설정하여 가중치를 제한합니다.
- 가중치의 노름(norm)이란 가중치 벡터(혹은 행렬)의 길이(length) 또는 크기(magnitude)를 측정하는 방법입니다.
- 목적 함수(Objective function)는 여러 분야에서 사용되는 단어이지만 머신러닝에서는 보통 '모델이 학습을 통해 최적화하고자 하는 함수'라고 해석합니다. 앞에서 제가 정리한 내용에서 대부분의 모델은 손실 함수(Loss function)를 최소화하는 방향으로 학습을 진행하였기 때문에 목적 함수가 곧 손실 함수이어서 별다른 구분 없이 넘어갔습니다. (대부분 목적 함수와 손실 함수를 따로 구별하지 않는 것 같습니다.)

<벡터(vector)의 노름(norm)>
벡터의 Ln-노름은 다음과 같이 정의합니다.

머신러닝에서는 이 중 L1-노름과 L2-노름을 사용합니다. 이들은 각각 다음과 같이 나타낼 수 있습니다.

<행렬(matrix)의 노름(norm)>
행렬의 L1-노름과 L2-노름은 다음과 같이 정의합니다.

행렬의 L1-노름은 'absolute column sums', 행렬의 L2-노름은 'spectral radius of W'라고도 합니다.
사용하는 가중치의 노름의 종류에 따라 규제의 종류가 정해집니다. 이때 L2 노름의 경우에는 제곱하여 더해줍니다.
- L1 규제(L1 Regularization) : 목적 함수 = 손실함수 + L1-norm term

- L2 규제(L2 Regularization) : 목적 함수 = 손실함수 + (L2-norm)
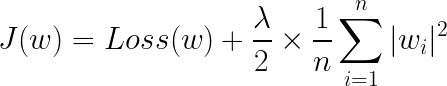
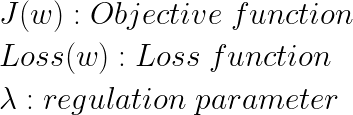
손실 함수 뒤에 더해지는 항을 페널티 항(penalty term)이라고도 합니다.
규제가 적용된 모델은 손실 함수와 가중치 벡터(또는 행렬)의 크기를 더한 목적 함수를 최소화하는 방향으로 학습을 하게 됩니다. 목적 함수가 최소화되기 때문에 손실 함수와 가중치 벡터(또는 행렬)의 크기 또한 필연적으로 최소화되겠죠. 따라서 가중치 벡터(또는 행렬) 내의 가중치들이 전부 작아지는 방향으로 모델이 학습이 됩니다. 가중치가 작아진다는 것은 곧 모델의 복잡도가 낮아진다는 것을 의미하므로 이는 과대 적합을 피하는 방향으로 학습이 된다는 것을 의미합니다.
regulation parameter는 규제의 정도를 제어하는 파라미터입니다. regulation parameter가 커지면 목적 함수를 최소화하는 과정에서 노름(norm)이 작아지므로 규제가 강해졌다고 하고, regulation parameter가 작아지면 반대로 규제가 약해졌다라고 할 수 있습니다. 과대 적합을 피하기 위해 규제를 사용할 때, 너무 큰 regulation parameter(즉, 강한 규제)를 사용하면 가중치가 제대로 학습되지 못해 과소 적합이 생길 수 있고, 너무 작은 regulation parameter(즉, 약한 규제)를 사용하면 과대 적합을 해결하지 못할 가능성이 있으므로 적절한 값을 선택하여 사용해야 합니다.
한 가지 살펴봐야 할 점은 규제를 할 때, 바이어스에 대한 규제는 따로 하지 않는다는 것입니다. 바이어스는 모델의 모양은 그대로 유지한 채 축을 따라 움직일 뿐이므로 규제를 적용하지 않습니다.
2) 라쏘 회귀(Lasso Regression)
라쏘 회귀(Lasso Regression)는 선형 회귀에 L1규제를 적용한 모델입니다.
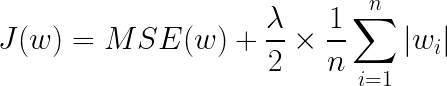
라쏘 모델에서 손실 함수 뒤의 페널티항은 L1노름과 regulation parameter 곱해져 있는 형태입니다. 만일 regulation parameter의 값이 커진다면 L1노름은 0에 가까워지게 됩니다.
경사 하강법을 적용하기 위해 목적함수를 w로 미분해보겠습니다. 손실 함수인 평균제곱오차(MSE)항은 가중치에 대해 미분이 가능하지만, 손실 함수 뒤 페널티 항은 가중치의 절댓값에 대한 식이므로 미분이 불가능합니다. 전 포스팅에서 컴퓨터는 미분을 할 때 보통 다음 방식을 통해 미분 값을 계산한다고 했습니다.
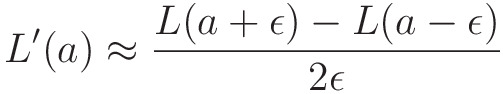
이를 이용하여 컴퓨터가 계산하는 절댓값 함수의 0에서의 미분계수를 구해보면 다음과 같습니다.
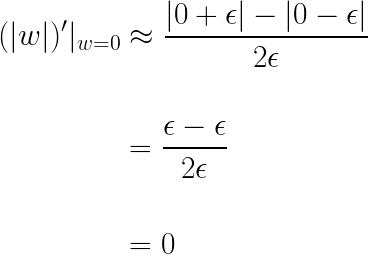
따라서 페널티 항의 가중치가 0일 때의 미분 값은 0이라고 생각해도 됩니다. 이제 목적 함수를 미분한 식을 살펴보면 다음과 같습니다.
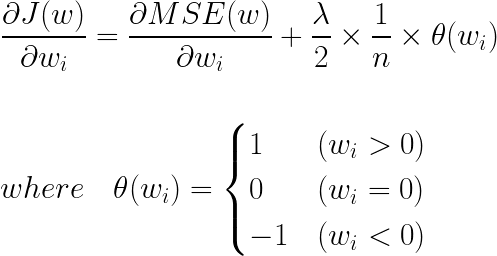
라쏘 회귀는 위의 식과 같이 상수값으로 모든 가중치를 깎아나갑니다(0이 되면 더 이상 깎지 않습니다). 즉, 규제가 강해지면(regulation parameter값이 커지면) L1-노름의 값이 작아지고, 이에 따라 모든 가중치들이 0이 되거나 0에 가까워집니다.
가중치가 0이 된다는 것은 모델에서 영향력이 작은 특성(feature)을 배제한다는 말과 같습니다. 즉, 중요하지 않은 특성들은 모델에서 제외하여 모델을 단순하게 만들고, 모델에서 가장 영향력이 큰(가장 중요한) 특성이 무엇인지 알게 해 주어 모델의 해석력이 좋아집니다.
3) 릿지 회귀(Ridge Regression)
릿지 회귀(Ridge Regression)는 선형 회귀에 L2-노름을 적용한 모델입니다.
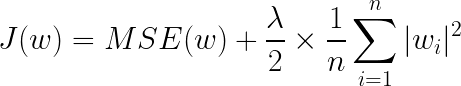
릿지 회귀는 라쏘 회귀와 비슷하지만 목적 함수가 가중치에 대한 미분이 가능하고, 한 번 미분하여도 가중치에 대한 항이 남아있다는 점에서 차이점이 있습니다. 즉, 릿지 회귀는 경사 하강법을 목적 함수에 적용할 때 값이 큰 가중치는 빠르게 작아지고, 값이 작은 가중치는 비교적 천천히 작아지게 해 줍니다.
따라서 라쏘 회귀와 달리 값이 0이 되는(제외하는) 가중치는 없지만, 가중치들이 골고루 0에 가까운 값으로 작아집니다. 모델의 가중치가 0에 가까워진다는 것은 모델의 편향이 증가하고 이에 따라 분산이 감소하는 것을 의미합니다. 즉, L2규제를 적용할 때 regulation parameter를 적절히 조절하면 모델의 과대 적합을 피할 수 있습니다.
L1규제와 L2규제는 모델의 과대적합을 피하는 아주 유용한 방법이 될 수 있습니다. 하지만 규제가 너무 강해지면 과소 적합을 야기할 수 있으므로 적절한 값을 선택하는 것이 중요합니다. L1규제와 L2규제의 장점만을 따온 Elastic Net이라는 모델도 있지만, 이는 다음 기회에 정리해보도록 하겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 신경망 (1) - 단층 퍼셉트론 (Single Layer Perceptron) (0) | 2021.11.21 |
|---|---|
| 분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 ) (0) | 2021.11.18 |
| 데이터 세트 (2) - 과대 적합(over fitting)과 과소 적합(under fitting) (0) | 2021.11.04 |
| 데이터 세트(1) - 훈련 세트(training set), 테스트 세트(test set), 검증 세트(validation set) (0) | 2021.11.01 |
| 분류 (4) - 다중 분류 (Multiclass Classification) 코드 구현 (0) | 2021.10.29 |




