머신러닝/딥러닝 공부
데이터 세트 (2) - 과대 적합(over fitting)과 과소 적합(under fitting) 본문
데이터 세트 (2) - 과대 적합(over fitting)과 과소 적합(under fitting)
호사린가마데라닌 2021. 11. 4. 01:33
머신러닝에서 과대 적합과 과소 적합은 모델의 성능을 낮추는 주된 원인입니다.
1 ) 과대 적합(over fitting)
과대 적합(over fitting)이란 모델이 훈련 세트에 과하게 적합한 상태가 되어 일반성이 떨어지는 현상입니다. 모델이 훈련 세트에 집착하여 학습을 하게 되는 것입니다.


위의 그림은 훈련 세트 내 데이터에 대해 적절한 모델을 빨간색, 과대 적합된 모델을 주황색으로 표현한 그림입니다. 과대 적합이 일어난 모델은 훈련 세트 내 모든 데이터를 섭렵하여 오차를 줄이려 하므로 주어진 훈련 세트 내 데이터에 대해서는 높은 정확도를 보여주지만 훈련 세트 외의 데이터에 대해서는 낮은 정확도를 보입니다. 즉, 기존 데이터의 규칙에 과하게 적응하여 새로운 데이터의 규칙을 잘 예측하지 못하는 것입니다.
따라서 과대 적합된 모델은 훈련 세트에 대해서는 좋은 성능을 갖는 것처럼 보이지만 검증 세트에서 낮은 성능을 갖습니다. 즉 모델을 학습시킬 때 어느 순간 이후로 모델의 훈련 세트에 대한 손실 값은 작아지지만 검증 세트에 대한 손실 값이 커진다면, 이는 모델이 훈련 세트에 밀착하여 학습이 진행되고 있다는 것, 즉 과대 적합을 의미합니다.
과대 적합의 발생 원인은 다양합니다.
- 데이터 세트 내 데이터가 충분하지 못한 경우
- 데이터 세트 내 분산이 크거나 노이즈가 심한 경우
- 모델의 복잡도가 큰 경우
- 과도하게 큰 epoch로 학습하는 경우
해결 방법은 상황마다 다릅니다.
- 가장 주된 원인은 데이터 세트가 충분히 크지 않은 경우입니다. 이런 경우 훈련 세트에 데이터를 추가하여 과대 적합을 줄일 수 있습니다.
- 더 이상의 데이터 확보가 어려울 경우 가중치를 제한하는 규제(Regularization)를 적용하여 모델의 복잡도를 낮추어 과대 적합을 완화하는 방법도 있습니다.
- 데이터 세트 내 데이터의 분산이 크거나 노이즈가 심한 경우 데이터를 전처리(preprocessing)하여 훈련에 적합한 데이터 세트로 바꿔줍니다.
- 또한 모델의 학습 곡선(learning curve)을 보고 적당한 epoch를 찾아내어 그 epoch까지만 훈련을 하도록 하는 방법도 존재합니다. 이를 조기종료(early-stopping)이라고 합니다.
*모델의 복잡도 : 쉽게 말해, 모델의 학습 가능한 가중치의 개수
2 ) 과소 적합(under fitting)
과소 적합(under fitting)은 반대로 모델이 훈련 세트의 규칙을 제대로 찾지 못해 모델의 성능이 낮게 나오는 현상입니다.


위의 그림은 훈련 세트 내 데이터에 대해 적절한 모델을 빨간색, 과소 적합된 모델을 주황색으로 표현한 그림입니다. 과소 적합이 일어난 모델은 모델의 복잡도가 낮아 훈련 세트 내 모든 데이터의 규칙을 제대로 찾아내지 못해 전체적으로 낮은 정확도를 보입니다.
과소 적합은 훈련 세트에 대한 손실값과 검증 세트에 대한 손실 값이 모두 크게 나타납니다. 즉, 훈련 세트에 대한 정확도와 검증 세트에 대한 정확도가 모두 낮은 경우입니다.
과소 적합의 원인은 다음과 같습니다.
- 모델의 복잡도가 낮은 경우
- 모델에 너무 많은 규제가 적용된 경우
- 충분하지 못한 epoch로 학습하는 경우
해결 방법은 상황에 따라 다릅니다.
- 모델의 복잡도가 낮은 경우 조금 더 복잡한 모델을 적용하여 훈련 세트의 규칙을 잘 찾아내도록 해줍니다.
- 모델에 너무 많은 규제가 걸린 경우 규제를 줄입니다.
- 더 많은 epoch를 통해 모델이 충분히 학습을 하여 훈련 세트의 규칙을 찾을 수 있도록 해줍니다.
3 ) 학습 곡선(learning curve)을 통한 과대 적합(over fitting)과 과소 적합(under fitting) 판단
학습 곡선(learning curve)이란 시간이나 시행 횟수에 따른 성취도를 표현한 그래프입니다. 다양한 분야에서 사용되는 단어지만 머신러닝에서는 보통 epoch에 따른 손실(loss)이나 정확도(accuracy)를 나타난 그래프라고 해석합니다.
이 학습 곡선을 그려보면 모델에게 과대 적합이나 과소 적합이 일어났는지 확인할 수 있습니다.
간단히 정리를 하면
- 과대 적합은 훈련 세트에서는 높은 정확도(낮은 손실)를, 검증 세트에서는 낮은 정확도(높은 손실)를 보였고,
- 과소 적합은 훈련 세트와 검증 세트 모두에서 낮은 정확도(높은 손실)를 보였습니다.
다음과 같은 학습 곡선이 있습니다.


왼쪽 학습 곡선에서 처음 몇 에포크 동안 검증 세트와 훈련 세트 모두 낮은 정확도를 보이고 있습니다. 즉, 과소 적합 현상이 나타나고 있네요. epoch가 증가함에 따라 모델의 정확도가 점점 증가하다가 어느 순간 훈련 세트의 정확도는 증가하지만 검증 세트의 정확도는 감소합니다. 이는 모델이 훈련 세트에 집착하여 학습을 하여 일반화된 규칙을 찾지 못하고 있다는 의미입니다. 즉, 과대 적합 현상이 나타나고 있습니다.
에포크에 따른 손실(loss)에 대한 그래프를 살펴보면 그래프가 위아래로 뒤집혔을 뿐, 똑같은 것을 의미한다는 것을 알 수 있습니다.
4 ) 편향 - 분산 트레이드 오프(bias-variance tradeoff)
입력값, 타깃, 모델이 내놓은 예측값을 다음과 같은 기호로 표현해보겠습니다.

이때 모델의 오차(error)는 다음과 같이 표현합니다.
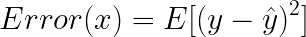
이 식을 변형해 보겠습니다.

이때 다음 식들을 각각 모델의 분산(variance)과 편향(bias)이라고 정의합니다.

여기서 시그마는 타깃(y)에 대한 분산입니다. 타깃은 건드릴 수 없는 값이므로 이 값을 '줄일 수 없는 오차(irreducible error)'라고 합니다.
위의 분산(variance)와 바이어스(bias)의 식에서 알 수 있듯이
-분산은 모델을 통과한 값들이 서로 얼마나 가까운지를 나타내는 지표이고
-편향(bias)은 모델을 통과한 값이 평균적으로 타깃과 얼마나 차이가 나는지를 나타내는 지표입니다.

과대 적합된 모델의 경우 예측값과 타깃의 차가 작으므로 편향이 작지만, 모델의 복잡도가 크기 때문에 분산이 큽니다.
반대로 과소 적합된 모델의 경우 모델의 복잡도가 낮아 분산이 작지만, 훈련 데이터의 적절한 규칙을 찾지 못해 타깃과의 차가 커 편향이 큽니다.
즉, 모델의 복잡도가 커질수록 모델의 분산은 커지고 편향은 작아집니다.
모델의 오차는 분산과 편향, 그리고 줄일 수 없는 오차가 더해져서 결정되므로, 합이 최소가 되는 적절한 분산과 편향을 찾아내야 합니다. 이를 '편향-분산 트레이드오프(bias-variance tradeoff)'이라고 합니다.
다음 포스팅에서는 과대 적합 문제를 해결하는 대표적인 방법 중 하나인 규제(regularization)와 로지스틱 회귀에 이 규제를 적용한 모델인 라쏘 모델(Lasso model)과 릿지 모델(Ridge model)에 대해서 정리해보겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 ) (0) | 2021.11.18 |
|---|---|
| 데이터 세트 (3) - 규제(Regularization), 라쏘 회귀(Lasso Regression)와 릿지 회귀(Ridge Regression) (0) | 2021.11.17 |
| 데이터 세트(1) - 훈련 세트(training set), 테스트 세트(test set), 검증 세트(validation set) (0) | 2021.11.01 |
| 분류 (4) - 다중 분류 (Multiclass Classification) 코드 구현 (0) | 2021.10.29 |
| 분류 (3) - 다중 분류(Multiclass Classification) (1) | 2021.10.26 |




