머신러닝/딥러닝 공부
분류 (6) - 다층 퍼셉트론 코드 (파이썬 구현) 본문
이번 포스팅에서는 파이썬으로 2개의 층을 가진 다층 퍼셉트론을 구현해보도록 하겠습니다. 또한 다음 포스팅에서는 이 코드를 이용하여 MNIST 숫자 손글씨 데이터 세트를 학습시켜 보고 단층 퍼셉트론과 어떤 차이가 있는지 살펴볼 생각입니다.
코드만 보고 싶으신 분은 밑의 '코드 보기'를 클릭해주세요.
class MultiLayer:
def __init__(self,learning_rate=0.01,batch_size=32,hidden_node=10):
self.w1=None #은닉층 가중치 행렬
self.b1=None #은닉층 바이어스 배열
self.w2=None #출력층 가중치 행렬
self.b2=None #출력층 바이어스 배열
self.lr=learning_rate #학습률
self.batch_size=batch_size
self.node=hidden_node #은닉층 노드 개수
self.losses=[] # 손실(훈련세트)
self.val_losses=[] # 손실(검증세트)
self.accuracy=[] # 정확도(훈련세트)
self.val_accuracy=[] # 정확도(검증세트)
def init_weights(self,m,n): # 가중치 초기화 함수
k=self.node
self.w1=np.random.normal(0,1,(m,k)) # 가우시안 분포로 초기화 (m x k) 행렬
self.b1=np.zeros(k) # 0으로 초기화
self.w2=np.random.normal(0,1,(k,n)) # 가우시안 분포로 초기화 (k x n) 행렬
self.b2=np.zeros(n) #0으로 초기화
def sigmoid(self,z1): #sigmoid 함수
z1=np.clip(z1,-100,None)
a1=1/(1+np.exp(-z1))
return a1
def softmax(self,z2): #softmax 함수
z2=np.clip(z2,-100,None)
exp_z2=np.exp(z2)
a2=exp_z2/np.sum(exp_z2,axis=1).reshape(-1,1)
return a2
def forward1(self,x): # 입력층 -> 은닉층 순전파
z1=np.dot(x,self.w1)+self.b1
return z1
def forward2(self,a1): # 은닉층 -> 출력층 순전파
z2=np.dot(a1,self.w2)+self.b2
return z2
def loss(self,x,y): # 손실 계산
z1=self.forward1(x)
a1=self.sigmoid(z1)
z2=self.forward2(a1)
a2=self.softmax(z2)
a2=np.clip(a2,1e-10,1-1e-10)
return -np.sum(y*np.log(a2)) #크로스 엔트로피
def backpropagation(self,x,y): # 역전파 알고리즘
z1=self.forward1(x)
a1=self.sigmoid(z1)
z2=self.forward2(a1)
a2=self.softmax(z2)
w2_grad=np.dot(a1.T,-(y-a2)) # 은닉층 가중치의 기울기 계산
b2_grad=np.sum(-(y-a2)) # 은닉층 바이어스의 기울기 계산
#은닉층으로 전파된 오차 계산
hidden_err=np.dot(-(y-a2),self.w2.T)*a1*(1-a1)
w1_grad=np.dot(x.T,hidden_err) # 입력층 가중치의 기울기 계산
b1_grad=np.sum(hidden_err,axis=0) #입력층 바이어스의 기울기 계산
return w1_grad,b1_grad,w2_grad,b2_grad
def minibatch(self,x,y):
iter=math.ceil(len(x)/self.batch_size)
x,y=shuffle(x,y)
for i in range(iter):
start=self.batch_size*i
end=self.batch_size*(i+1)
yield x[start:end],y[start:end]
def fit(self,x_data,y_data,epochs=40,x_val=None,y_val=None):
self.init_weights(x_data.shape[1],y_data.shape[1]) # 가중치 초기화
for epoch in range(epochs):
l=0 # 손실 누적할 변수
#가중치 누적할 변수들 초기화
for x,y in self.minibatch(x_data,y_data):
l+=self.loss(x,y) # 손실 누적
# 역전파 알고리즘을 이용하여 각 층의 가중치와 바이어스 기울기 계산
w1_grad,b1_grad,w2_grad,b2_grad=self.backpropagation(x,y)
# 은닉층 가중치와 바이어스 업데이트
self.w2-=self.lr*(w2_grad)/len(x)
self.b2-=self.lr*(b2_grad)/len(x)
# 입력층 가중치와 바이어스 업데이트
self.w1-=self.lr*(w1_grad)/len(x)
self.b1-=self.lr*(b1_grad)/len(x)
#검증 손실 계산
val_loss=self.val_loss(x_val,y_val)
self.losses.append(l/len(y_data))
self.val_losses.append(val_loss)
self.accuracy.append(self.score(x_data,y_data))
self.val_accuracy.append(self.score(x_val,y_val))
print(f'epoch({epoch+1}) ===> loss : {l/len(y_data):.5f} | val_loss : {val_loss:.5f}',\
f' | accuracy : {self.score(x_data,y_data):.5f} | val_accuracy : {self.score(x_val,y_val):.5f}')
def predict(self,x_data):
z1=self.forward1(x_data)
a1=self.sigmoid(z1)
z2=self.forward2(a1)
return np.argmax(z2,axis=1) #가장 큰 인덱스 반환
def score(self,x_data,y_data):
return np.mean(self.predict(x_data)==np.argmax(y_data,axis=1))
def val_loss(self,x_val,y_val): # 검증 손실 계산
val_loss=self.loss(x_val,y_val)
return val_loss/len(y_val)
1 ) 모델의 구조
먼저 이 모델이 어떤 구조를 갖는지 확인해보겠습니다. 이 모델은 m개의 특성을 가진 데이터를 입력으로 받은 다음 k개의 노드를 가진 은닉층을 거쳐 원-핫 인코딩을 통해 n개의 라벨 중 하나를 택하여 예측값을 내놓습니다. 입력층에서 은닉층으로 넘어갈 때는 활성화 함수로 sigmoid함수를 사용하였고, 은닉층에서 출력층으로 넘어갈 때는 softmax함수를 사용하였습니다.
모델의 구조를 그림으로 표현하면 다음과 같습니다.
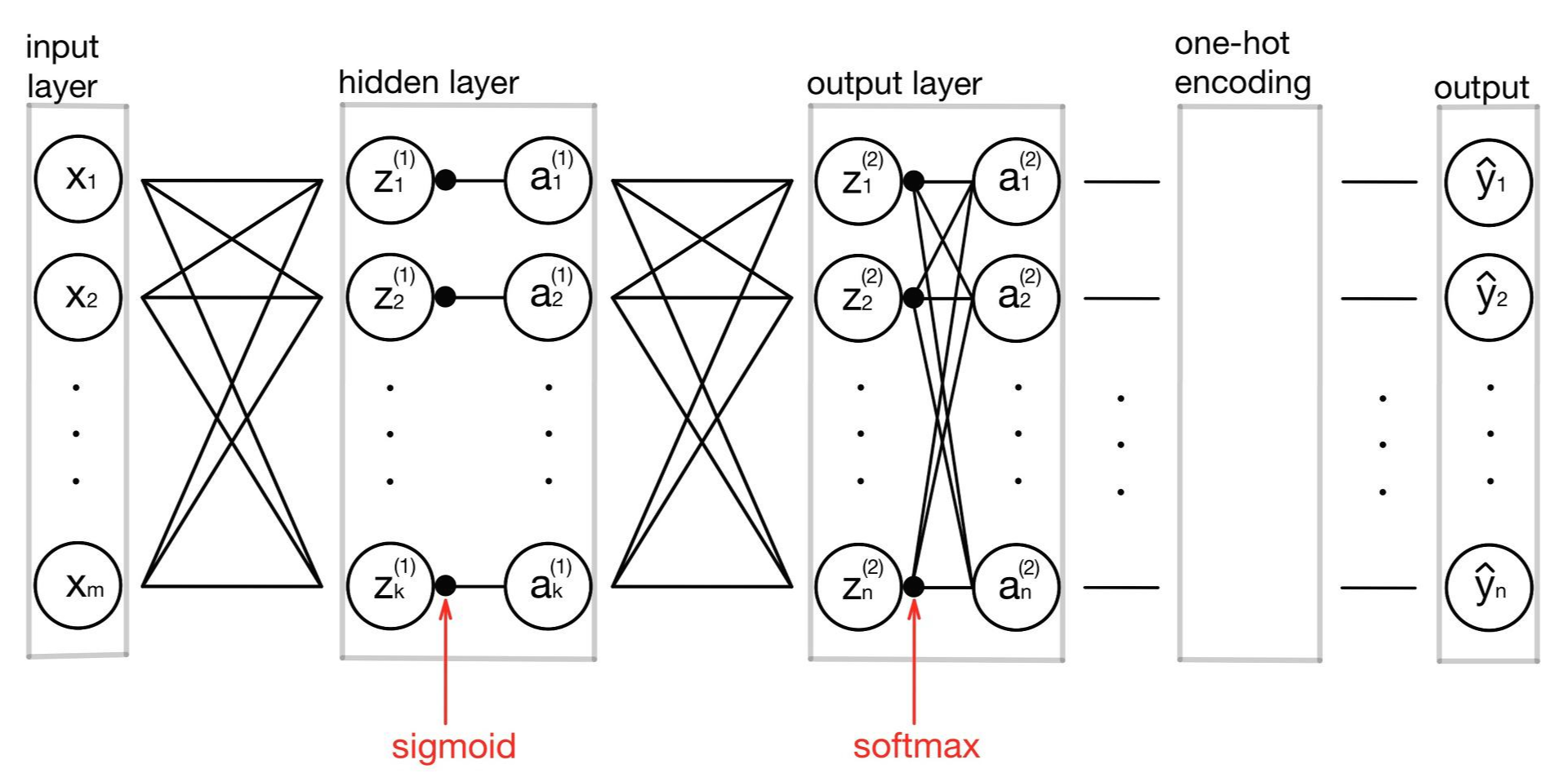
이 그림을 단순하게 표현해보자면 다음과 같습니다.
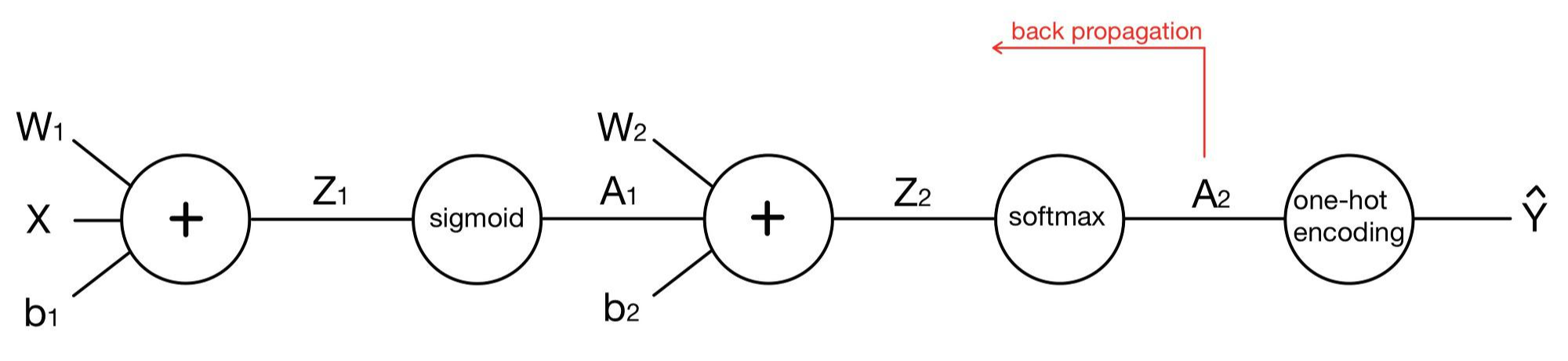
이제 코드를 살펴보겠습니다. 기본적인 구조는 단층 퍼셉트론과 똑같지만, 층이 하나 늘어나면서 가중치와 바이어스가 하나씩 더 생겼습니다. 따라서 앞에서 구현했던 코드에 필요한 부분을 채우는 식으로 코드를 짜보았습니다. 층이 하나인 다중 분류 모델의 코드는 아래의 포스팅에서 확인할 수 있습니다.
https://yhyun225.tistory.com/19
분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 )
1) 다중 분류 모델 코드 이전 포스팅에서 수정했던 다중 분류 코드를 가져오겠습니다. https://yhyun225.tistory.com/15?category=964332 분류 (4) - 다중 분류 (Multiclass Classification) 코드 구현 다중 분류..
yhyun225.tistory.com
먼저 클래스의 생성자 부분입니다.
class MultiLayer:
def __init__(self,learning_rate=0.01,batch_size=32,hidden_node=10):
self.w1=None #은닉층 가중치 행렬
self.b1=None #은닉층 바이어스 배열
self.w2=None #출력층 가중치 행렬
self.b2=None #출력층 바이어스 배열
self.lr=learning_rate #학습률
self.batch_size=batch_size #미니배치 크기
self.node=hidden_node #은닉층 노드 개수
self.losses=[] # 손실(훈련세트)
self.val_losses=[] # 손실(검증세트)
self.accuracy=[] # 정확도(훈련세트)
self.val_accuracy=[] # 정확도(검증세트)가중치와 바이어스의 개수를 늘려주었고, node라는 변수에 은닉층에 있는 노드의 개수(self.node)를 저장합니다. 또한 학습 데이터가 많아질수록 경사 하강법을 사용하기 힘드므로 미니 배치 경사 하강법도 구현하려 합니다. 이를 위해 self.batch_size도 추가해주었습니다. 마지막으로 훈련 세트와 검증 세트에 대한 정확도를 저장할 리스트도 추가했습니다.
가중치와 바이어스를 초기화해주는 함수도 따로 구현해주겠습니다. 가중치는 표준 가우시안 분포 N(0,1)로, 바이어스는 0으로 초기화해줍니다.
def init_weights(self,m,n): # 가중치 초기화 함수
k=self.node
self.w1=np.random.normal(0,1,(m,k)) # 가우시안 분포로 초기화 (m x k) 행렬
self.b1=np.zeros(k) # 0으로 초기화
self.w2=np.random.normal(0,1,(k,n)) # 가우시안 분포로 초기화 (k x n) 행렬
self.b2=np.zeros(n) #0으로 초기화
첫 번째 층에서 활성화 함수로 쓰일 sigmoid함수와, 두 번째 층에서 활성화 함수로 쓰일 softmax함수를 구현해주어야 합니다.
def sigmoid(self,z1): #sigmoid 함수
z1=np.clip(z1,-100,None)
a1=1/(1+np.exp(-z1))
return a1
def softmax(self,z2): #softmax 함수
z2=np.clip(z2,-100,None)
exp_z2=np.exp(z2)
a2=exp_z2/np.sum(exp_z2,axis=1).reshape(-1,1)
return a2
순전파(feed forward)와 손실을 계산해주는 함수를 구현해줍니다. 순전파는 입력층에서 은닉층으로 전파하는 foward1() 함수와 은닉층에서 출력층으로 전파하는 forward2()함수를 나누어 구현해주었습니다. 손실 함수는 교차 엔트로피(cross entropy)를 사용하였습니다.
def forward1(self,x): # 입력층 -> 은닉층 순전파
z1=np.dot(x,self.w1)+self.b1
return z1
def forward2(self,a1): # 은닉층 -> 출력층 순전파
z2=np.dot(a1,self.w2)+self.b2
return z2
def loss(self,x,y): # 손실 계산
z1=self.forward1(x)
a1=self.sigmoid(z1)
z2=self.forward2(a1)
a2=self.softmax(z2)
a2=np.clip(a2,1e-10,1-1e-10) #로그 안에 0이 들어가는 것을 방지
return -np.sum(y*np.log(a2)) #크로스 엔트로피
이제 역전파 알고리즘(BackPropagation)에 대한 코드인데, 그전에 먼저 기울기(도함수)를 계산해주도록 하겠습니다. 먼저 W2와 b2의 기울기를 계산해보겠습니다. 다음과 같은 식을 통해 구할 수 있습니다.
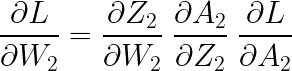
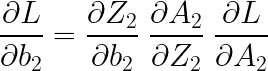
각각의 기울기를 살펴보면 다음과 같습니다.
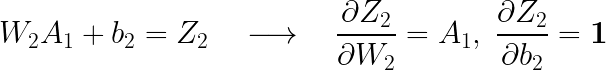
(여기서 볼드체 숫자 1은 모든 원소가 1로 구성된 행렬입니다. )
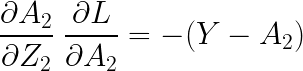
(위의 수식에 대한 설명은 아래 포스팅에서 이미 진행하였으므로 생략하였습니다)
https://yhyun225.tistory.com/14
분류 (3) - 다중 분류(Multiclass Classification)
이진 분류(Binary Classification)는 타깃의 값이 어떤 기준에 대하여 참(True) 또는 거짓(False)의 값을 가졌습니다. 다중 분류(Multiclass Classification)의 경우 타깃이 가질 수 있는 값이 3개 이상입니다. 타..
yhyun225.tistory.com
따라서 은닉층의 가중치와 바이어스의 기울기는 다음과 같이 구할 수 있습니다.
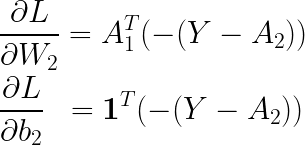
이번에는 입력층의 가중치와 바이어스에 대한 기울기를 보겠습니다.
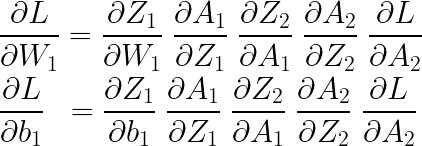
마찬가지 방식으로 각각의 기울기를 구해보면,
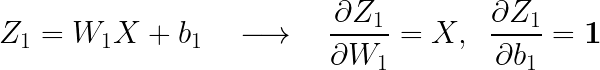
(bold체로 표기한 1입니다)
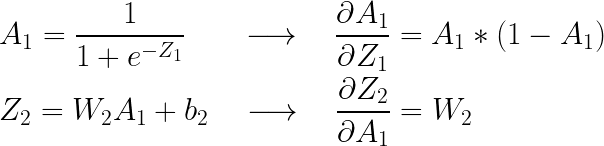
( 별(*)은 원소별 곱을 의미합니다)
이고, 위에서 구했던 기울기가 그대로 나왔으므로
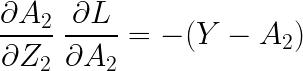
입니다. 모든 기울기를 종합하여 곱해주어야 하는데, 행렬의 곱을 신경 써서 곱해주어야 합니다. 이는 다음과 같습니다.
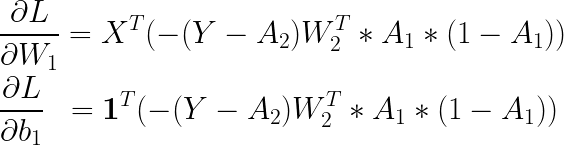
뒤에 공통으로 반복되는 부분을 '은닉층으로 전파된 오차'라 하고 hidden_err라 이름을 붙여주었습니다. 위의 내용을 코드로 구현해보면 아래와 같습니다.
def backpropagation(self,x,y): # 역전파 알고리즘
z1=self.forward1(x) #입력층 -> 은닉층 순전파
a1=self.sigmoid(z1) #시그모이드 함수
z2=self.forward2(a1) #은닉층 -> 출력층 순전파
a2=self.softmax(z2) #소프트맥스 함수
w2_grad=np.dot(a1.T,-(y-a2)) # 은닉층 가중치의 기울기 계산
b2_grad=np.sum(-(y-a2)) # 은닉층 바이어스의 기울기 계산
#은닉층으로 전파된 오차 계산
hidden_err=np.dot(-(y-a2),self.w2.T)*a1*(1-a1)
w1_grad=np.dot(x.T,hidden_err) # 입력층 가중치의 기울기 계산
b1_grad=np.sum(hidden_err,axis=0) #입력층 바이어스의 기울기 계산
return w1_grad,b1_grad,w2_grad,b2_grad
다음은 미니 배치 경사 하강법(SGD)을 구현하기 위해 입력받은 데이터를 배치 단위로 나눠주는 함수를 구현하겠습니다.
def minibatch(self,x,y):
iter=math.ceil(len(x)/self.batch_size)
x,y=shuffle(x,y)
for i in range(iter):
start=self.batch_size*i
end=self.batch_size*(i+1)
yield x[start:end],y[start:end]먼저 한 에포크 동안 몇 번의 반복(iteration)이 필요한지 계산해주어야 합니다. 이는 math모듈의 ceil 메소드를 이용하여 구해주었습니다. 그다음 전체 데이터셋을 섞어주는데, 이는 배치마다 데이터를 골고루 포함하게끔 해주기 위함입니다. 마지막으로 for문을 이용하여 입력받은 batch_size 만큼씩 데이터셋을 나누어줍니다.
주어진 데이터에 대해 미니 배치 경사 하강법을 이용하여 모델을 학습시키는 코드입니다.
def fit(self,x_data,y_data,epochs=40,x_val=None,y_val=None):
self.init_weights(x_data.shape[1],y_data.shape[1]) # 가중치 초기화
for epoch in range(epochs):
l=0 # 손실 누적할 변수
#가중치 누적할 변수들 초기화
for x,y in self.minibatch(x_data,y_data):
l+=self.loss(x,y) # 손실 누적
# 역전파 알고리즘을 이용하여 각 층의 가중치와 바이어스 기울기 계산
w1_grad,b1_grad,w2_grad,b2_grad=self.backpropagation(x,y)
# 은닉층 가중치와 바이어스 업데이트
self.w2-=self.lr*(w2_grad)/len(x)
self.b2-=self.lr*(b2_grad)/len(x)
# 입력층 가중치와 바이어스 업데이트
self.w1-=self.lr*(w1_grad)/len(x)
self.b1-=self.lr*(b1_grad)/len(x)
#검증 손실 계산
val_loss=self.val_loss(x_val,y_val)
self.losses.append(l/len(y_data))
self.val_losses.append(val_loss)
self.accuracy.append(self.score(x_data,y_data))
self.val_accuracy.append(self.score(x_val,y_val))기존의 코드와 달라진 점은 미니 배치 경사 하강법을 이용한다는 것입니다. 기존에는 입력받은 데이터에서 데이터 하나씩 뽑아 하나하나 계산하여 기울기를 누적하였지만(경사 하강법을 사용했기 때문에 전체 데이터셋을 한 번에 이용하면 속도가 매우 느립니다) 지금은 배치 단위로 나누어서 기울기를 계산하기 때문에 배치 내 데이터 전부를 행렬로 처리하여 기울기를 계산해줍니다. 또한 마지막에 추가로 모델의 정확도를 저장하는 코드를 추가하였습니다.
마지막으로 predict(), score(), val_loss() 함수들인데, 이들 또한 기존의 함수와 달라진 점이 거의 없습니다.
def predict(self,x_data):
z1=self.forward1(x_data)
a1=self.sigmoid(z1)
z2=self.forward2(a1)
return np.argmax(z2,axis=1) #가장 큰 인덱스 반환
def score(self,x_data,y_data):
return np.mean(self.predict(x_data)==np.argmax(y_data,axis=1))
def val_loss(self,x_val,y_val): # 검증 손실 계산
val_loss=self.loss(x_val,y_val)
return val_loss/len(y_val)
이로써 층을 2개 갖는(은닉층이 1개인) 다층 퍼셉트론의 코드 구현이 끝났습니다. 다음 포스팅에서는 이 모델을 이용하여 MNIST숫자 손글씨 데이터 세트를 학습시켜보겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 분류 (7) - MNIST 숫자 손글씨 분류 모델 (다층 퍼셉트론) (0) | 2021.12.02 |
|---|---|
| 신경망 (3) - 역전파 알고리즘(BackPropagation algorithm) (1) | 2021.11.25 |
| 신경망 (2) - 다층 퍼셉트론(Multi Layer Perceptron)과 활성화 함수(Activation function) (0) | 2021.11.22 |
| 신경망 (1) - 단층 퍼셉트론 (Single Layer Perceptron) (0) | 2021.11.21 |
| 분류(5) - MNIST 숫자 손글씨 분류 모델( 다중 선형 분류 ) (0) | 2021.11.18 |




