머신러닝/딥러닝 공부
분류 (1) - 이진 분류(Binary Classification)와 로지스틱 회귀(Logistic Regression) 본문
분류 (1) - 이진 분류(Binary Classification)와 로지스틱 회귀(Logistic Regression)
호사린가마데라닌 2021. 10. 20. 23:59분류 모델은 데이터를 분류하는 방법을 학습합니다. 분류 모델은 크게 이진 분류(Binary Classification)와 다중 분류(Multi Classification)로 나뉩니다.
- 이진 분류(Binary Classification)는 입력값에 따라 모델이 분류한 카테고리가 두 가지인 분류 알고리즘입니다. 주로 어떤 대상에 대한 규칙이 참(True)인지 거짓(False)인지를 분류하는데 쓰입니다. 예를 들어 암 종양을 분류하는 모델은 어떤 종양을 입력으로 받았을 때 이 종양이 암 종양인지(True) 암 종양이 아닌지(False) 분류합니다.
- 다중 분류(Multi Classification)은 입력값에 따라 모델이 분류한 카테고리가 세 가지 이상인 분류 알고리즘입니다. 예를 들어 숫자 손글씨를 분류하는 모델(0~9까지 10개의 카테고리를 갖습니다) 등이 있습니다.
이번 포스팅에서는 이진 분류에서 가장 대표적인 알고리즘인 로지스틱 회귀(Logistic Regression)에 대해 정리해보겠습니다. 이름에는 회귀가 들어갔지만 이 알고리즘은 분류 알고리즘에 속합니다.
1) 로지스틱 회귀(Logistic Regression)의 발전사
로지스틱 회귀 알고리즘의 시초라 할 수 있는 퍼셉트론(Perceptron) 알고리즘은 1957년 프랑크 로젠블라트(Frank Rosenblatt)라는 미국의 심리학자가 제안하였습니다. 퍼셉트론은 신경 세포 뉴런과 유사한 동작을 하는 알고리즘입니다. 간단히 설명하면 뉴런은 신호를 받아들인 뒤 임계치를 넘으면 다음 뉴런에 신호를 전달합니다.
퍼셉트론은 입력받은 데이터를 이용하여 선형 방정식을 통해 값을 계산하고, 계단 함수(step function)를 이용하여 그 값이 임계치 이상이라면 참(True==1)을, 미만이라면 거짓(False==0)을 반환합니다. 퍼셉트론의 구조는 다음과 같이 생겼습니다.

퍼셉트론은 선형 회귀 모델과 같은 방식으로 입력에 가중치를 곱한뒤 더하여 z값을 계산하고, z값이 양수라면 참(True)을, 음수라면 거짓(False)을 반환합니다. 또한 계단 함수를 통과한 값을 토대로 역전파 알고리즘(Back Propagation)을 이용하여 가중치들과 바이어스를 업데이트합니다. 역전파 알고리즘에 대해서는 추후에 설명하도록 하겠습니다. 계단 함수는 다음과 같이 생긴 함수입니다.

퍼셉트론은 가중치의 업데이트가 계단 함수를 통과한뒤에 일어납니다. 하지만 계단 함수를 통과한 값들은 -1과 1이라서 연속적인(Continuous) 손실 함수를 사용할 수 없다는 단점이 있습니다. 이를 개선한 것이 바로 1960년 버나드 위드로우(Bernard Widrow)와 테드 호프(Tedd Hoff)가 발표한 적응형 선형 뉴런(Adaptive Linear Neuron) 혹은 아달린(Adaline)입니다. 아달린은 계단 함수를 통과하기 전 데이터를 이용하여 가중치를 업데이트하기 때문에 연속적인 손실 함수를 사용할 수 있다는 장점이 있습니다. 아달린은 다음 그림과 같은 방식으로 구성됩니다.

마지막으로 이 아달린에 활성화 함수(Activation function)를 추가한 모델이 바로 로지스틱 회귀(Logistic Regression)입니다. 활성화 함수에 대해서는 추후에 좀 더 자세히 정리하도록 하겠습니다. 지금은 활성화 함수를 사용하는 이유는 '선형인 데이터를 비선형으로 바꾸기 위해서'라고만 말씀드리겠습니다. 로지스틱 회귀의 구조는 아래 그림과 같습니다.

가운데에 추가된 활성화 함수가 z의 값을 다른 값 a로 바꿔주는 것을 확인할 수 있습니다. 그리고 이 a를 이용하여 가중치를 업데이트 해줍니다. threshold function은 퍼셉트론이나 아달린의 계단 함수와 비슷한 역할을 하지만 활성화 함수로 바뀐 값(a)을 이용하여 예측값을 출력합니다.
그럼 로지스틱 회귀는 활성화 함수로 어떤 함수를 사용할까요?
2) 시그모이드(Sigmoid) 함수
시그모이드 함수에 대해 정리하기 전에 먼저 정리할 내용이 있습니다. 바로 '오즈 비(odds ratio)'입니다. 오즈 비는 성공 확률과 실패 확률의 비율로, 다음과 같이 정의합니다.

여기서 p는 성공확률을 뜻합니다. 이 오즈 비에 자연로그 함수를 취한 함수를 로짓 함수(logit function)라고 정의합니다.

로짓 함수는 아래의 그래프와 같이 생겼습니다.
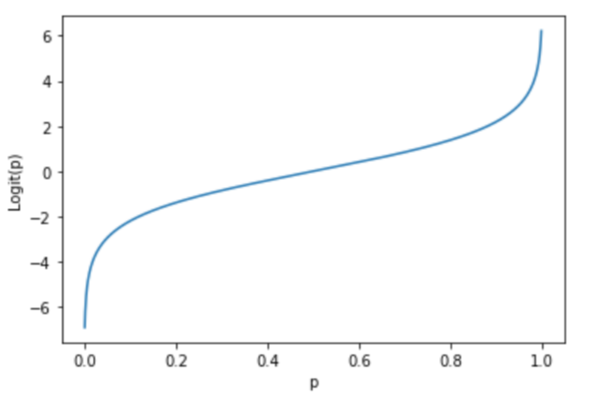
그래프에서 알 수 있다시피 p값이 0으로 다가가면 로짓 함수의 값은 음의 무한대로 발산하고, p값이 1로 다가가면 로짓 함수의 값은 양의 무한대로 발산합니다. 이제 로짓 함수를 z라 정의하고 z에 대해 정리해보겠습니다. z에 대해 정리해주는 이유는 x축을 z로 가져가지 위해서입니다.
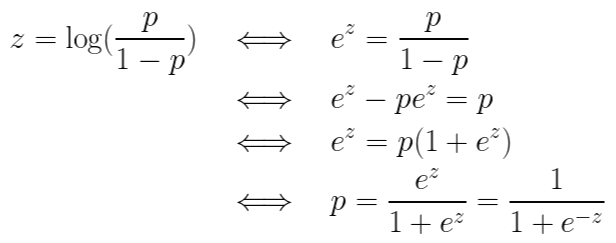
이렇게 완성된 식이 바로 시그모이드 함수(sigmoid function)입니다. 시그모이드 함수를 그려보면 다음과 같습니다.
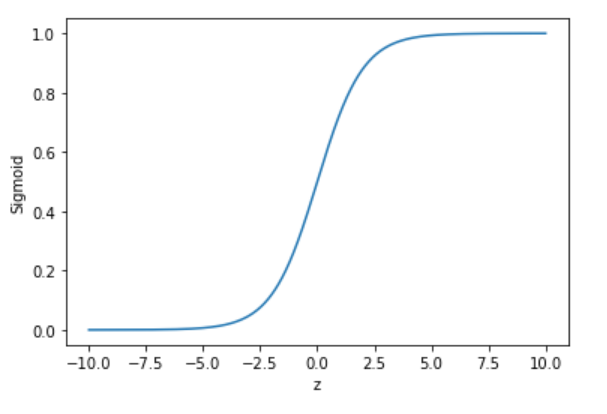
시그모이드 함수는 모든 z값에 대해 0과 1 사이의 함숫값을 가집니다. z가 0일 때는 함숫값으로 0.5를 갖습니다. 그러면 이제 시그모이드 함수를 왜 사용하는지 알 수 있겠네요. 로지스틱 회귀 모델은 입력값과 가중치를 곱해 나온 값(z)을 활성화 함수에 대입하고, 활성화 함수를 통과한 값(a)이 임계치 이상이면 참(True)을, 이하면 거짓(False)을 반환하다고 했습니다. 활성화 함수를 시그모이드 함수로 사용하면 활성화 함수를 통과한 값(a)이 0부터 1까지의 값을 갖기 때문에 이를 확률처럼 해석할 수 있게 됩니다. 만일 '참(True) 일 확률이 60%(0.6)인 경우에 대해서만 참(True)으로 분류'하는 모델을 만든다면 임계 함수에서의 임계치만 0.6으로 수정해 주면 되겠죠.
2) 로지스틱 회귀의 손실 함수
앞에서 정리한 회귀 모델의 경우 손실 함수로 MSE(Mean Squre Error)를 사용하였습니다. 로지스틱 회귀의 경우 손실 함수로 이진 교차 엔트로피(Binary Cross-Entropy)를 사용합니다. 이 함수는 다음과 같은 형태입니다.

a는 활성화 함수를 통과한 값입니다. 타깃, 즉 y값은 0 또는 1이기 때문에 i번째 데이터에 대한 손실은 다음과 같은 값을 가집니다.
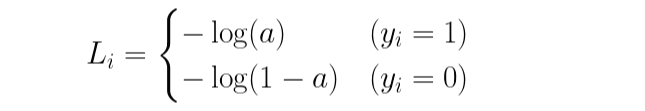
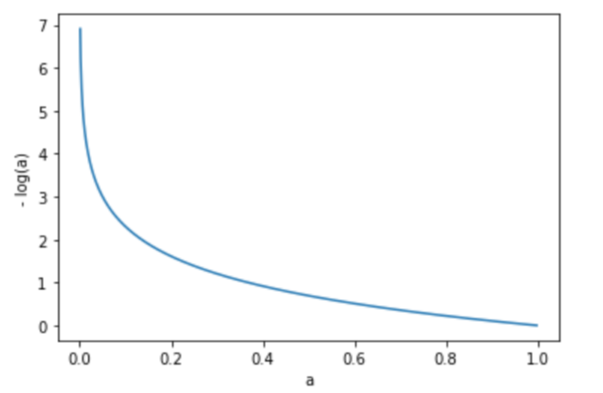
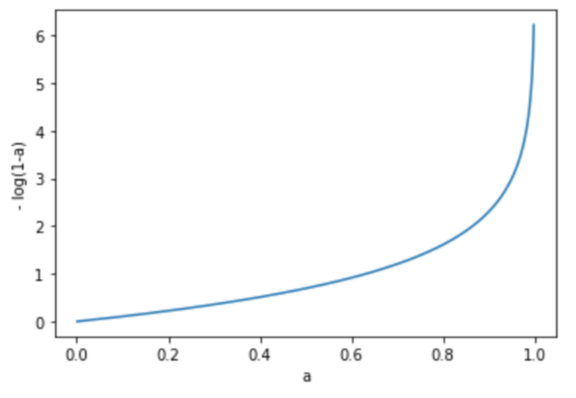
시그모이드 함수를 통과하고 나온 a는 0부터 1까지의 값을 가졌었습니다. 위의 그래프는 각각 -log(a)의 그래프와 -log(1-a)의 그래프를 그린 것입니다. 그래프에서 알 수 있듯이 -log(a)는 a값이 1에 가까워질수록 그 값이 작아집니다. 반대로 -log(1-a)의 그래프는 a값이 0에 가까워질수록 값이 작아집니다.
즉 손실 함수의 값을 최소화하는 과정에서 타깃이 참(True)이라면 -log(a)의 값이 작아져 a값이 1에 가까워지고, 타깃이 거짓(False)이라면 -log(1-a)의 값이 작아져 a값이 0에 가까워지게 됩니다. 이제 마지막으로 손실 함수의 값을 최소로 만들기 위해 가중치와 바이어스를 찾아야 합니다.
3) 경사하강법 적용
경사하강법을 적용하여 가중치와 절편을 업데이트하려면 먼저 손실 함수에 대한 가중치와 바이어스의 기울기를 구해야 합니다. 이를 구하는 과정에서 연쇄 법칙(chain rule)을 적용합니다.
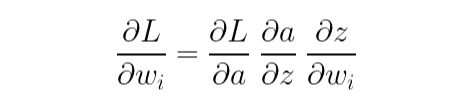
단계별로 어떤 식으로 가중치를 구하게 되는지 살펴보겠습니다.
- 처음에 입력값(x)과 가중치(w)를 선형 방정식에 대입하여 z를 구했습니다. 즉 z에 대한 w와 b의 기울기를 구할 수 있습니다.

- 다음에는 z를 시그모이드 함수에 통과시켜 a를 얻었습니다. 즉 a에 대한 z의 기울기를 구할 수 있습니다.
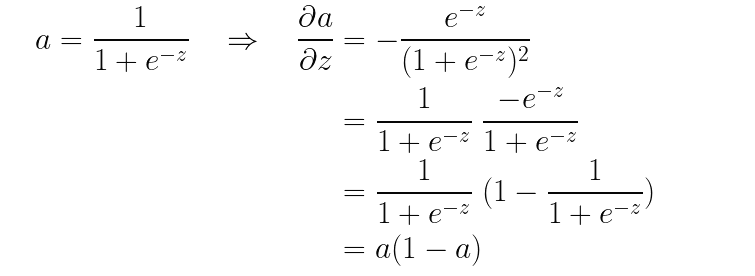
- 마지막으로 이진 교차 엔트로피와 a값을 이용하여 오차를 정의했었습니다.
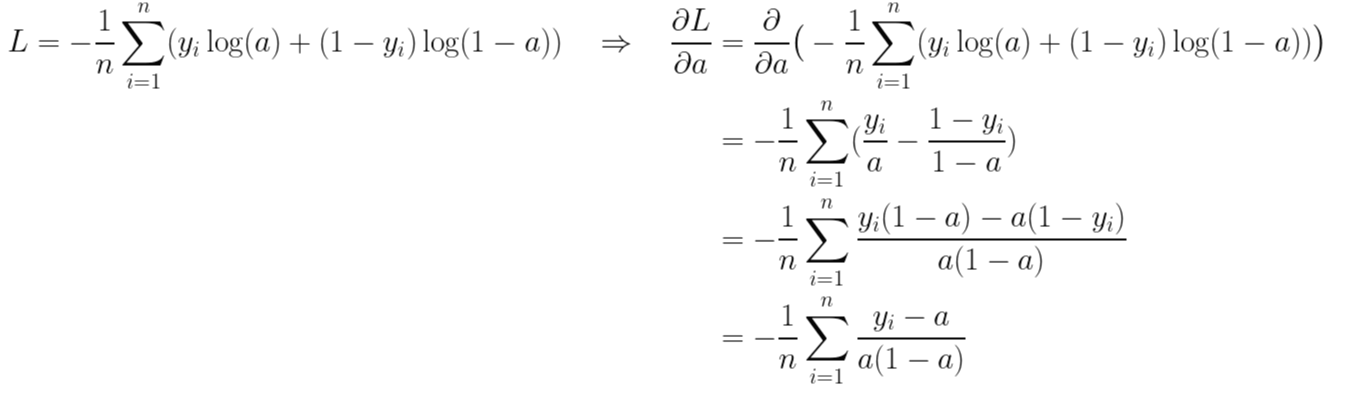
이제 손실함수에 대한 가중치의 기울기를 구할 수 있겠군요.
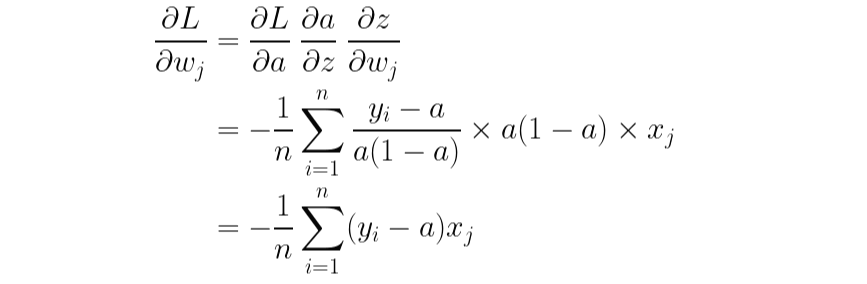
똑같은 방법으로 바이어스에 대한 기울기도 구할 수 있습니다.
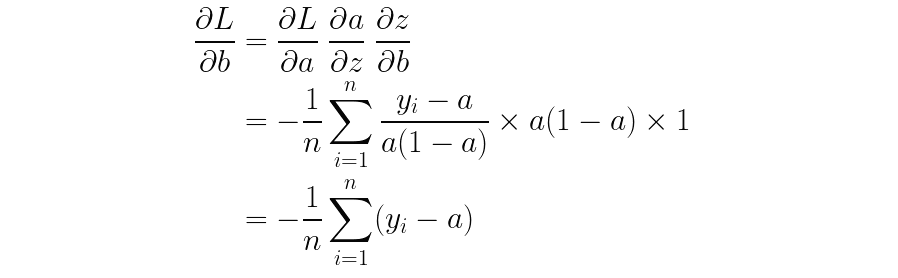
마찬가지로, index i와 j를 헷갈리면 안 됩니다. i는 모든 데이터에 대하여 오차를 더하는 의미에서 사용한 index이고, j는 임의의 j번째 가중치에 대한 기울기를 구하기 위해 사용한 index입니다.
형태를 보니 MSE에 대한 가중치와 바이어스의 기울기와 매우 유사합니다. 지금까지 정리한 내용을 합치면 다음과 같은 방식으로 가중치와 바이어스를 업데이트할 수 있다는 것을 알 수 있습니다.

수식이 잔뜩 나왔지만 결국 같은 내용의 반복입니다. 이제 로지스틱 회귀의 뼈대를 세웠으니 다음 포스팅에서는 구글 코랩에서 직접 코드로 로지스틱 회귀를 구현해보도록 하겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 분류 (3) - 다중 분류(Multiclass Classification) (1) | 2021.10.26 |
|---|---|
| 분류 (2) - 위스콘신 유방암 데이터 세트(Wisconsin breast cancer dataset) (0) | 2021.10.21 |
| 회귀 (3) - 당뇨병 환자 데이터(diabetes)와 다중 선형 회귀(Multi Regression Model) (1) | 2021.10.19 |
| 회귀 (2) - 다중 선형 회귀 (Multi Linear Regression) (1) | 2021.10.18 |
| 회귀 (1) - 단순 선형 회귀(Simple Linear Regression) (2) | 2021.10.17 |




