머신러닝/딥러닝 공부
회귀 (1) - 단순 선형 회귀(Simple Linear Regression) 본문
1 ) 회귀(Regression)
회귀 모델은 주어진 데이터로 학습시켜 연속적인 예측값을 출력하는 모델입니다.
회귀 모델은 크게 선형 회귀 모델(Linear Regression)과 비선형 회귀 모델(Non-Linear Regression)로 나눌 수 있습니다. 여기서 선형(Linear)이란 다음의 성질을 만족시키는 것입니다.



선형의 성질을 만족시키지 못하면 비선형(Non-Linear)이라고 부릅니다.
가장 간단한 선형 회귀 모델은 다음과 같은 모양입니다.

또한 다음과 같은 모양도 선형 모델이라 할 수 있겠네요.

이처럼 변수의 개수만 달라질 뿐 모델이 선형이라는 성질을 가지고 있는 것에는 변함이 없습니다. 모델의 형태를 보면 결국 직선, 혹은 평면, 그리고 4차원 이상의 공간에서는 초평면(hyperplane)이 될 것입니다. 따라서 선형 회귀 모델은 결국 데이터를 표현하는 차원의 공간에서, 데이터들과 이루는 오차가 가장 작은 직선 혹은 평면(초평면)을 찾는 모델이라고 할 수 있습니다.
이 중 데이터가 2차원의 공간에서 표현이 되어 회귀 모델이 단순한 직선 형태가 되면 단순 선형 회귀(Simple Linear Regression), 그 이상의 공간에서 평면 혹은 초평면의 형태가 된다면 다중 선형 회귀(Multi Linear Regression)이라고 합니다.
사실 저희가 인지할 수 있는 차원은 3차원까지이고 그 이후의 차원에 대해서는 머리로 이해하기가 매우 힘이 듭니다. 하지만 차원 수에 상관없이 모델을 최적화하는 방법은 동일하므로 4차원 이상의 데이터를 다루는 모델에 대해서도 같은 방식으로 학습을 합니다.
이번 포스팅에서는 회귀 모델 중에서도 선형 회귀 모델, 그중에서도 단순 선형 회귀 모델을 다뤄보도록 하겠습니다.
2 ) 단순 선형 회귀(Simple Linear Regression)
2차원 평면에 다음과 같은 점들이 있습니다.

다음의 점들을 가장 잘 표현할 수 있는 선은 어떤 형태일까요? 아마 사람은 직관적으로 아래 그림의 빨간 직선이 점들을 잘 표현한다고 말할 것입니다.

하지만 컴퓨터는 우리처럼 직관적으로 선을 찾아내지 못합니다. 지금부터 선형 회귀 모델을 학습시켜 저 데이터들을 가장 잘 표현하는 식을 찾아보겠습니다. 앞에서 다뤘던 내용에서 오차를 정의하기 위한 손실 함수로 MSE(Mean Square Error)를, 모델의 오차를 줄이기 위해 사용하는 옵티마이저로 BGD(경사하강법)를 사용하도록 하겠습니다.


경사하강법을 적용하기 위해서 손실 함수의 weight와 bias에 대한 기울기를 계산할 필요가 있습니다. 먼저 w에 대한 기울기를 식으로 정리해 보면 다음과 같습니다.

bias에 대한 기울기도 마찬가지 방법으로 구해줍니다.

즉 다음과 같이 weight와 bias에 대한 손실 함수의 기울기를 이용하여 손실 함수의 최솟값을 찾아가면 되겠네요.
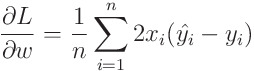

이제 모델을 코드로 구현해보도록 하겠습니다.
머신러닝을 공부할 때 여러 선택지가 있겠지만 저는 파이썬을 이용해서 모델을 작성하고 실행을 시킵니다. 앞으로도 파이썬을 이용한 코드를 올릴 예정입니다. 실행 환경은 구글 코랩입니다.
우리가 사용하는 모델은 선형 회귀 모델이고, 데이터가 2차원 상의 공간에서 분포하기 때문에 직선 형태의 함수가 되면 되겠죠. 즉, 아래의 식이 우리가 구하고자 하는 모델이 될 것입니다.

우리의 목적은 주어진 입력값(x)과 타깃(y)에 가장 적합한 w와 b값을 찾는 것입니다.
주어진 input 데이터에 대하여 예측값을 계산해야 하기 때문에 forward함수를 지정하여 예측값을 구해줍니다. forward 함수는 데이터가 모델을 통과하여 움직이는 방향이 앞(forward)이기 때문에 이름을 이렇게 지었습니다.
def forward(x):
y_pred=x*w+b
return y_pred
또한 각 입력값에 대하여 에포크마다 모델이 얼마만큼의 손실, 즉 오차를 갖는지 측정하기 위해 loss함수도 정의해주도록 하겠습니다.
def loss(x,y):
y_pred=forward(x)
return (y_pred-y)**2
마지막으로 위에서 계산하였던 w와 b의 기울기도 함수로 정의해주도록 하겠습니다.
def gradient(x,y):
y_pred=forward(x)
w_grad=2*x*(y_pred-y)
b_grad=2*(y_pred-y)
return w_grad,b_grad
이제 모델을 학습시켜 보도록 하겠습니다. 초기 가중치를 1, 바이어스를 0으로 주고, 0.1의 학습률로 20 에포크 동안 학습하도록 진행시켰습니다. 코드의 x_data와 y_data는 각각 input과 target의 값을 담고 있는 numpy배열입니다.
#초기값 설정(initialization)
w=1.0
b=0.0
#에포크와 학습률 지정
epochs=20
learning_rate=0.1
for epoch in range(epochs): # 20에포크 동안 모델이 학습을 진행
l=0 # 매 에포크마다 발생한 손실 측정
w_grad=0 #경사하강법의 w의 기울기
b_grad=0 #경사하강법의 b의 기울기
for x,y in zip(x_data,y_data):
l+=loss(x,y) # x_data의 모든 x에 대한 각각의 손실값을 누적함
w_i,b_i=gradient(x,y)
w_grad+=w_i # w값 누적
b_grad+=b_i # b값 누적
w-=learning_rate*(w_grad/len(y_data)) # weight 업데이트
b-=learning_rate*(b_grad/len(y_data)) # bias 업데이트
print(f'epoch ({epoch+1})===> loss : {l/len(y_data):.4f} | weight : {w:.4f} | bias : {b:.4f}')
위 코드를 실행시킨 결과는 아래와 같습니다.

에포크가 진행될때마다 처음에는 빠르게(큰 간격), 그 후로 천천히(작은 간격) 작아지고 있는 것을 확인할 수 있습니다. 즉, 우리가 만든 선형 회귀 모델이 주어진 데이터에 맞게 학습되고 있습니다. 20 에포크 후 직선이 어떤 형태를 하고 있는지 확인해보겠습니다. 아래의 초록 선이 바로 우리가 학습시킨 모델입니다.
import matplotlib.pyplot as plt
point1=(0,b) #직선의 시작점
point2=(1.5,1.5*w+b) #직선의 끝점
plt.plot([point1[0],point2[0]],[point1[1],point2[1]],'g') #지정한 두점을 잇는 직선
plt.scatter(x_data,y_data) # x_data와 y_data 상의 점을 2차원 평면에 찍어줌
plt.xlabel('x data')
plt.ylabel('y data')
plt.show()
이제 주어진 데이터를 잘 표현하고 있네요.
하지만 뭔가 모델이라는 객체를 학습시킨 느낌이 아닙니다. 이제 위의 코드를 토대로 선형 회귀 모델을 파이썬의 클래스를 이용하여 작성해보겠습니다. 앞으로도 여러 모델에 대해 정리할 예정인데, 제가 쓰는 모든 코드에서 모델은 객체로 생성합니다.
SimpleLinear이라는 클래스를 생성해 준 뒤, 생성자를 설정해줍니다. forward함수, loss함수, gradient함수는 위와 같은 내용으로, 클래스 내부의 함수로 작성해주었습니다.
class SimpleLinear:
def __init__(self,learning_rate=0.001):
self.w=None #가중치
self.b=None #바이어스
self.lr=learning_rate #모델의 학습률
self.losses=[] #에포크마다 저장할 손실값 변화량 리스트
self.weight_history=[] #에포크마다 저장할 가중치 변화량 리스트
self.bias_history=[] #에포크마다 저장할 바이어스 변화량 리스트
def forward(self,x):
y_pred=self.w*x+self.b
return y_pred
def loss(self,x,y):
y_pred=self.forward(x)
return (y_pred-y)**2
def gradient(self,x,y):
y_pred=self.forward(x)
w_grad=2*x*(y_pred-y)
b_grad=2*(y_pred-y)
return w_grad,b_grad
모델을 학습시키는 함수는 fit함수로, input으로 받은 입력값들과 타깃들을 토대로 학습을 진행합니다. 마찬가지로 weight와 bias는 각각 1과 0으로 초기화시켜주었습니다.
def fit(self,x_data,y_data,epochs=20):
self.w=1.0
self.b=0.0
for epoch in range(epochs):
l=0 #손실
w_grad=0 #경사하강법의 w의 기울기
b_grad=0 #경사하강법의 b의 기울기
for x,y in zip(x_data,y_data):
l+=self.loss(x,y)
w_i,b_i=self.gradient(x,y) #i번째 데이터에 대한 가중치와 바이어스의 기울기 계산
w_grad+=w_i #w값 누적
b_grad+=b_i #b값 누적
self.w-=self.lr*(w_grad/len(y_data)) #w 없데이트
self.b-=self.lr*(b_grad/len(y_data)) #b 업데이트
self.losses.append(l/len(y_data)) #매 에포크마다 손실 값 기록
self.weight_history.append(self.w) #매 에포크마다 w값 기록
self.bias_history.append(self.b) #매 에포크마다 b값 기록
print(f'epoch ({epoch+1})===> loss : {l/len(y_data):.4f} | weight : {self.w:.4f} | bias : {self.b:.4f}')
위에서 학습시킬때와 달라진 점이 있다면 매 에포크 후 업데이트된 weight와 bias를 모델 내부의 history 변수에 저장한다는 것입니다. 이제 이 모델 객체를 생성한 후, input값들과 target들로 학습을 시켜보겠습니다. 학습률은 0.1로 주었습니다.
model=Linear(learning_rate=0.1)
model.fit(x_data,y_data)
실행 결과는 아래와 같습니다.

아까와 마찬가지로 학습이 잘 되는 것을 확인할 수 있습니다.
이 모델의 손실값이 어떻게 변하는지 확인해보겠습니다.
plt.plot(model.losses)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
처음 3 에포크까지는 빠른 속도로 최솟값에 수렴하다가 이후로 천천히 수렴하네요. 이는 앞에서 정리했던 경사하강법이 보이는 특징입니다. 우리가 학습시킨 선형 회귀 모델은 경사하강법을 옵티마이저로 채택했으니 당연한 현상입니다.
weight와 bias의 변화 양상도 볼까요?
plt.plot(model.weight_history)
plt.xlabel('epoch')
plt.ylabel('weight')
plt.show()
weight 또한 3 에포크까지는 빠르게 어느 값으로 수렴하다가 그 이후로 천천히 수렴합니다.
plt.plot(model.bias_history)
plt.xlabel('epoch')
plt.ylabel('bias')
plt.show()
bias도 동일한 수렴 양상을 보여줍니다.
사실 제가 학습에 사용한 데이터는 아래의 코드에서 볼 수 있듯이 y=3x+2 직선에 노이즈(노이즈는 표준정규분포를 따르도록 했습니다)를 적용하여 0부터 1.5까지 임의로 200개를 뽑아낸 점들입니다.
import numpy as np
x_data=1.5*np.random.rand(200)
y_data=x_data*3+2+np.random.randn(200)
위에서 훈련시킨 모델의 weight는 약 3.01로, bias는 약 2.05로 수렴하고 있었으니 꽤나 학습이 잘된것 같습니다.
다음 포스팅에서는 2차원 이상의 데이터들로 학습을 하는 다중 선형 회귀 모델 (Multi Linear Regression Model)에 대하여 정리해보도록 하겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 회귀 (3) - 당뇨병 환자 데이터(diabetes)와 다중 선형 회귀(Multi Regression Model) (1) | 2021.10.19 |
|---|---|
| 회귀 (2) - 다중 선형 회귀 (Multi Linear Regression) (1) | 2021.10.18 |
| 머신러닝 - 회귀(Regression) VS 분류(Classification) (0) | 2021.10.13 |
| 모델이 학습하는 방법 (3) - 확률적 경사하강법(Stochastic Gradient Descent, SGD)와 미니배치 경사하강법(mini-batch Gradient Descent) (0) | 2021.10.13 |
| 모델이 학습하는 방법 (2) - 경사하강법의 한계 (1) | 2021.10.12 |



