머신러닝/딥러닝 공부
회귀 (2) - 다중 선형 회귀 (Multi Linear Regression) 본문
이전 포스팅에서는 단순 선형 회귀 모델에 대해 정리해보았습니다. 단순 선형 회귀 모델은 2차원 상의 데이터들을 대상으로 가장 적합한 직선을 찾는 모델이었습니다. 하지만 모든 데이터가 2차원에 존재하지는 않습니다.
예를 들어 어떤 사람이 자신에게 가장 좋은 집을 찾아 점수를 예측하는 프로그램을 작성한다고 생각해봅시다. 가장 좋은 집의 기준이 무엇일까요? 아마도 사람마다 다르겠지만 집의 평수, 화장실의 개수, 역세권 유무, 소음 차단이 잘되는지, 단지 내에 공원이 있는지, 회사에서 집이 가까운지 등등 여러 조건이 있을 것입니다. 이런 경우 프로그램에 input으로 주어야 할 데이터의 크기가 2개 이상이 되어버립니다. 즉, 아래와 같이 예측값을 내놓기 위해 필요한 가중치의 개수가 증가할 것입니다.

위의 식을 벡터를 이용하여 다음과 같이 표현할 수 있습니다. (벡터와 스칼라를 구분짓기 위해 벡터를 볼드체로 표현했습니다.)


이처럼 2차 이상의 차원에서 정의된 데이터들을 가장 잘 표현하는 평면이나 초평면을 찾는 것이 바로 다중 선형 회귀 모델입니다. 단순 선형 회귀 모델과 마찬가지로 손실 함수로 MSE를, 옵티마이저로 BGD를 채택하여 가중치를 업데이트해 보겠습니다. 한 가지 유의해야 할 점은 가중치가 벡터이기 때문에 앞의 방법처럼 바로 미분을 적용해서 기울기를 구할 수 없습니다. 3차원 이상의 공간에서 가중치를 업데이트하기 위해서는 가중치의 현재 위치에서의 기울기 벡터(gradient)를 구해야 합니다. gradient는 다음과 같이 정의합니다.

따라서 기존의 BGD는 다음과 같은 형태로 가중치를 업데이트 하면 됩니다.

그런데 아래의 식을 보겠습니다.

index i와 j를 헷갈리면 안됩니다. i는 모든 데이터에 대한 오차의 합을 나타내기 위해 사용한 index이고, j는 임의의 가중치에 대한 손실 함수의 기울기를 계산하기 위해 사용한 index입니다.
MSE에 대한 각 가중치의 편미분이 2차원에서 MSE에 대한 가중치의 편미분과 완전히 일치합니다. 다만 다중 선형 회귀 모델은 여러개의 가중치를 가지기 때문에 각각의 가중치에 대해 업데이트를 해주어야 합니다.
즉, 다음과 같은 방식으로 업데이트를 해주어야 합니다.

이제 마지막으로 벡터를 이용하여 간단하게 정리하겠습니다.
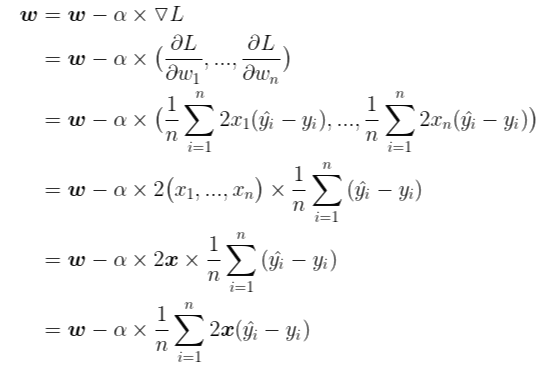
이렇게 보니 단순 선형 회귀 모델에서 적용했던 경사하강법과 형태가 완전히 같은 것이 실감이 납니다. 단지 입력받는 데이터가 n차원이다 보니 벡터를 사용하는 점 빼고는 전부 똑같습니다. 이제 코드로 직접 구현을 해보겠습니다.
이번에는 다음과 같이 3차원 상에 200개의 데이터가 존재합니다. 이 3차원 상의 점들을 가장 잘 표현하는 선형 회귀 모델, 즉 평면을 찾는 것이 목표입니다.

3차원 공간이기 때문에 모델의 수식은 다음과 같습니다.

평면을 찾기 위해 MultiLinear라는 클래스를 작성하도록 하겠습니다.
class MultiLinear:
def __init__(self,learning_rate=0.001):
self.w=None #모델의 weight 벡터 self.w=(w_1,w_2)
self.b=None #모델의 bias
self.lr=learning_rate #모델의 학습률
self.losses=[] #매 에포크마다 손실을 저장하기 위한 리스트
self.weight_history=[] #매 에포크마다 계산된 weight를 저장하기 위한 리스트
self.bias_history=[] #매 에포크마다 계산된 bias를 저장하기 위한 리스트
def forward(self,x):
y_pred=np.sum(x*self.w)+self.b #np.sum함수는 인자로 받은 numpy배열의 모든 원소의 합을 return합니다.
return y_pred
def loss(self,x,y):
y_pred=self.forward(x)
return (y_pred-y)**2
def gradient(self,x,y):
y_pred=self.forward(x)
w_grad=2*x*(y_pred-y)
b_grad=2*(y_pred-y)
return w_grad,b_grad
앞서 다뤘던 단순 선형 회귀 모델과 비슷하지만 forward함수에서 약간의 차이가 있습니다. 이 모델은 입력값으로 받는 x데이터가 벡터(정확히는 numpy배열)이므로 모델의 가중치 벡터와 x데이터의 내적(inner product)을 계산해주어야 합니다. np.sum() 함수는 인자로 받은 numpy배열의 모든 원소들의 합을 계산해주는 함수입니다.
def fit(self,x_data,y_data,epochs=20):
self.w=np.ones(2) #모델의 weight들을 전부 1로 초기화
self.b=0 #모델의 bias를 0으로 초기화
for epoch in range(epochs):
l=0 #계산할 손실값
w_grad=np.zeros(2) #weight의 기울기를 누적할 numpy배열
b_grad=0 #bias의 기울기를 누적할 변수
for x,y in zip(x_data,y_data):
l+=self.loss(x,y)
w_i,b_i=self.gradient(x,y)
w_grad+=w_i #weight누적
b_grad+=b_i #bias누적
self.w-=self.lr*(w_grad/len(y_data)) #weight 업데이트
self.b-=self.lr*(b_grad/len(y_data)) #bias 업데이트
print(f'epoch ({epoch+1}) loss : {l/len(y_data):.4f} | weight1 : {self.w[0]:.4f} | weight2 : {self.w[1]:.4f} | bias : {self.b:.4f}')
self.losses.append(l/len(y_data)) #손실값 저장
self.weight_history.append(self.w) #weight 배열 저장
self.bias_history.append(self.b) #bias값 저장
모델을 학습시키는 함수인 fit함수도 단순 선형 회귀 모델과 똑같습니다. 마찬가지로 차이라면 처음 가중치들을 초기화할때 np.ones() 함수를 이용하여 모든 가중치들을 1로 초기화한다는 점이 있겠네요. 다른 부분은 스칼라 계산이 벡터의 계산으로 바뀌었을 뿐, 전부 동일합니다.
이제 모델 객체를 생성한 뒤 40에포크 동안 학습을 진행시켜보겠습니다. x_data와 y_data는 각각 위의 그림의 3차원 공간의 점들의 좌표들에 대한 내용을 담고 있는 np배열입니다. 학습률은 0.1로 설정했습니다.
model=MultiLinear(learning_rate=0.1)
model.fit(x_data,y_data,epochs=40)
아래는 결과입니다.


손실값이 3 에포크까지는 빠르게 작아지다가 이후 천천히 작아지는 것을 확인할 수 있습니다. 이는 경사하강법을 옵티마이저로 채택했기에 당연한 결과입니다. 가중치들과 바이어스도 어떤 값에 수렴하는 것을 확인할 수 있네요.
이 모델이 표현하는 평면을 확인해보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#평면을 구성할 grid생성
x=np.linspace(0,1.5,10)
y=np.linspace(0,1.5,10)
x,y=np.meshgrid(x,y)
#모델의 가중치를 이용하여 평면의 방정식 표현
z=model.w[0]*x+model.w[1]*y+model.b
#3차원 그림
fig=plt.figure()
ax=fig.gca(projection='3d')
ax.view_init(25,50)
ax.plot_surface(x,y,z,alpha=1.0,cmap=plt.cm.coolwarm)
ax.scatter(x_data[:,0],x_data[:,1],y_data,marker='o',s=10)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
plt.show()
잘 보이지 않네요. 평면 위의 점들은 빨간색으로, 평면 아래 점들은 초록색으로 그려보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#평면을 구성할 grid생성
x=np.linspace(0,1.5,10)
y=np.linspace(0,1.5,10)
x,y=np.meshgrid(x,y)
#모델의 가중치를 이용하여 평면의 방정식 표현
z=model.w[0]*x+model.w[1]*y+model.b
#3차원 그림
fig=plt.figure()
ax=fig.gca(projection='3d')
for x_,y_ in zip(x_data,y_data):
#모델의 예측값이 y값보다 큰 경우 초록색으로 칠합니다
if model.w[0]*x_[0]+model.w[1]*x_[1]+model.b>y_:
ax.scatter(x_[0],x_[1],y_,color='g',marker='o',s=10)
#모델의 예측값이 y값보다 작은 경우 빨간색으로 칠합니다.
else:
ax.scatter(x_[0],x_[1],y_,color='r',marker='o',s=10)
ax.view_init(25,50)
ax.plot_surface(x,y,z,alpha=1.0,cmap=plt.cm.coolwarm)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
plt.show()
이렇게 보니 데이터들이 모델(평면)을 기준으로 적절하게 나뉘네요.
사실 아래의 코드를 보면 알겠지만 이 데이터는 제가 y=2x_1+3x_2+2 평면 위의 임의의 200개의 점들에 표준정규분포를 따르는 노이즈를 추가한 데이터입니다. 위에서 모델의 w_1은 약 2.08로, w_2는 약 3.15로, b는 약 1.9로 수렴하고 있었으니 나름대로 평면을 잘 찾아내네요.
import numpy as np
x_data=1.5*np.random.rand(200,2)
y_data=x_data[:,0]*2+x_data[:,1]*3+2+np.random.randn(200)
이로써 다중 선형 회귀 모델에 대해서도 정리를 해보았습니다. 단순 선형 회귀 모델과 다중 선형 회귀 모델은 다루는 데이터의 차원이 다를 뿐, 기본적인 경사하강법의 원리와 모델 파라미터(가중치와 바이어스)를 업데이트하는 과정은 똑같은 것을 알 수 있습니다.
다음으로 사이킷런(scikit-learn)에서 제공하는 당뇨병 환자의 데이터 세트를 활용하여 선형 회귀 모델을 구축한뒤에 분류 모델로 넘어가도록 하겠습니다.



