머신러닝/딥러닝 공부
분류 (3) - 다중 분류(Multiclass Classification) 본문
이진 분류(Binary Classification)는 타깃의 값이 어떤 기준에 대하여 참(True) 또는 거짓(False)의 값을 가졌습니다. 다중 분류(Multiclass Classification)의 경우 타깃이 가질 수 있는 값이 3개 이상입니다. 타깃이 가지는 값에 대응되는 데이터의 모임을 클래스(class) 혹은 레이블(label)이라고 하기도 합니다. 다중 분류의 경우 단일 레이블 분류(single-label classification)에 속합니다. 즉, 입력값 하나당 하나의 클래스에만 대응될 수 있습니다. 이와 반대로 하나의 입력값이 여러 개의 클래스에 대응되는 경우 다중 레이블 분류(multi-label classification)이라고 합니다.
예를 들어 숫자는 0부터 9까지 총 10개가 있습니다. 만일 손으로 쓴 숫자 데이터 세트에 대하여
- 입력으로 받은 숫자 사진이 0인지 아닌지 분류하는 것은 이진 분류 모델을,
- 입력으로 받은 숫자 사진이 0부터 9 중 어떤 숫자인지 분류하는 것은 다중 분류 모델을 사용합니다.
로지스틱 회귀의 경우 다음의 그림과 같이 표현했었습니다.

입력값의 특성(feature)과 중간 연산의 결과를 하나의 노드(node)처럼 생각하고, 활성화 함수를 간략하게 표현하기 위해 활성화 함수를 작은 원으로 그리겠습니다.

로지스틱 회귀 모델을 이런 식으로 표현한 이유는 층(layer)이라는 개념을 표현하기 위해서입니다. 층(layer)에 대해서는 추후에 딥러닝의 인공 신경망(artificial neural network)에 대해 정리할 때 좀 더 자세하게 다루도록 하겠습니다. 이런 표현 방식은 신경망을 표현할 때 빈번히 사용되는 방식입니다. 이제 다중 분류 모델이 어떻게 생겼는지 보겠습니다.

로지스틱 회귀의 구조와 비슷하게 생겼지만 몇 가지 달라진 점이 있습니다.
로지스틱 회귀의 경우 참(True) 또는 거짓(False)을 판별하기 때문에 출력 값이 하나였지만, 다중 분류 모델은 타깃의 종류가 여러 개이기 때문에 출력 값도 여러 개입니다. 각각의 출력 값은 그에 대응하는 타깃과 매칭 될 확률을 나타냅니다. 로지스틱 회귀에서는 선형 방정식을 통과한 값을 sigmoid함수를 이용하여 가공했으나, 다중 분류는 softmax함수를 사용하고 있습니다. 마지막으로 로지스틱 회귀에서는 마지막에 나온 a값이 임계치를 넘는지에 따라 참과 거짓을 판별하기 위해 threshold function을 이용했지만 다중 분류 모델에서는 함수는 one-hot encoding이라는 기법을 사용하고 있습니다.
이들이 각각 무엇인지 알아보도록 하겠습니다.
1) 소프트맥스(softmax) 함수와 원-핫 인코딩(one-hot-encoding)
소프트 맥스 함수는 다음과 같이 생겼습니다.
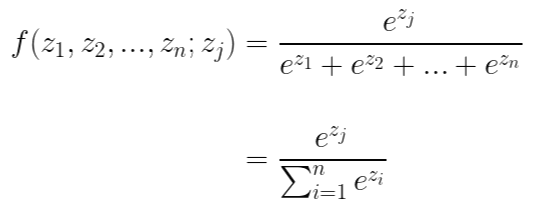
왜 이렇게 생겼는지 유도하는 과정은 추후에 올리도록 하겠습니다.
소프트 맥스 함수는 시그모이드 함수를 일반화한 함수로서 시그모이드 함수처럼 결괏값을 확률처럼 해석할 수 있게 해 줍니다. 즉, 입력값에 따라 중구난방으로 튀는 값들을 0부터 1 사이의 숫자들로 정규화시켜줍니다. 또한 위의 수식을 보면 알 수 있듯이 출력으로 나온 값들의 합이 1이므로 확률처럼 서로 다른 입력값에 대해서도 비교할 수 있게 해 줍니다.
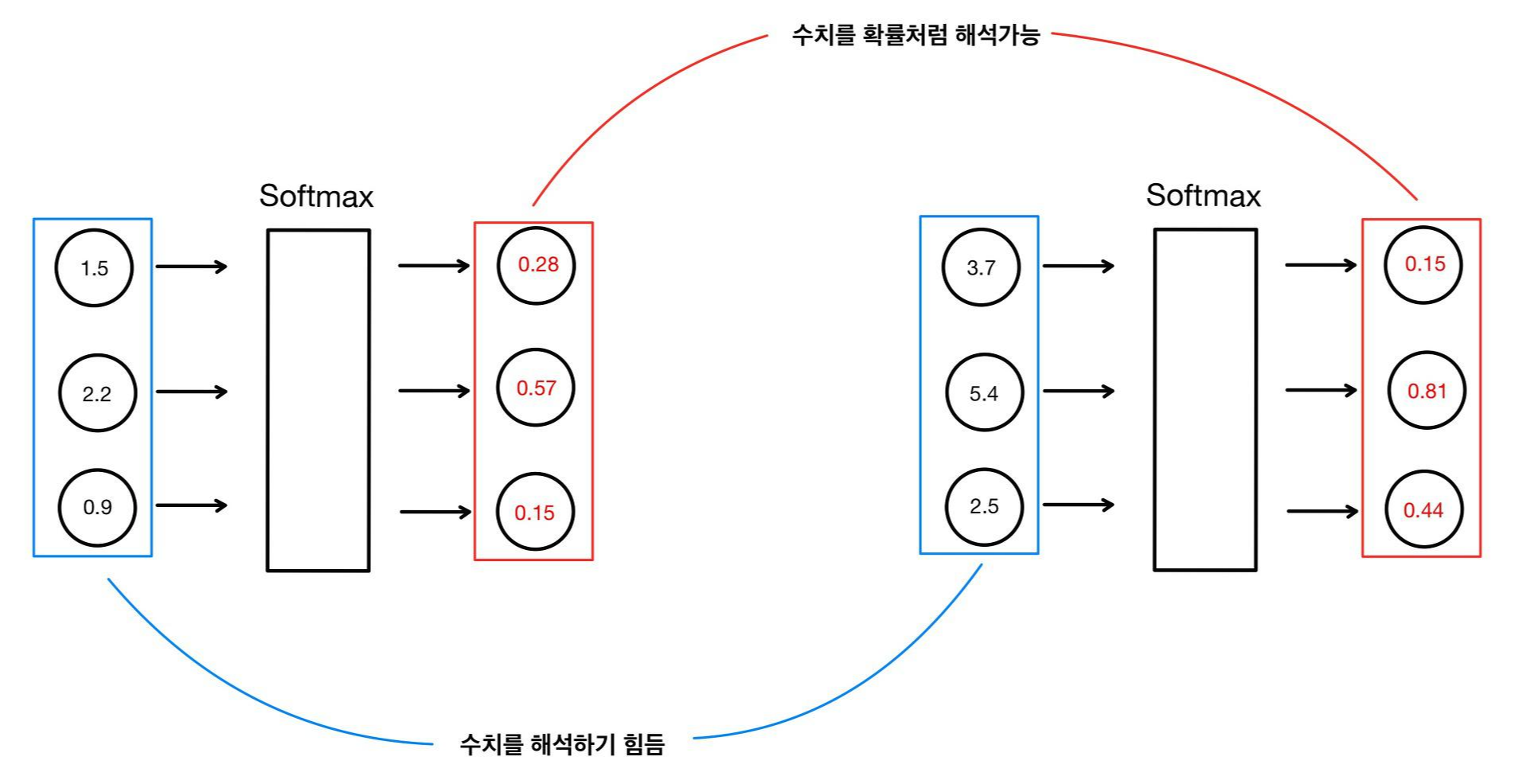
그림의 softmax함수를 통과한 값들은 합이 1인 것을 확인할 수 있습니다. softmax함수를 통과하기 전의 값들만 보고 두 데이터를 비교하는 것은 거의 불가능하지만, softmax를 통과한 뒤 값들은 확률 값처럼 생각할 수 있기에 비교하는 것은 쉽습니다. 첫 번째 그림은 57%의 확률로 두 번째 타깃일 가능성이 높고, 두 번째 그림은 81%의 확률로 두번째두 번째 타깃일 가능성이 높으므로 두 번째 데이터가 좀 더 높은 신뢰성을 가지고 있습니다. softmax함수는 시그모이드 함수와 데이터의 특성의 개수만 다를 뿐, 같은 역할을 하고 있습니다. (사실 softmax함수는 sigmoid함수의 generalized version입니다.)
여기서 softmax함수를 통과한 값들 중 가장 높은 값에 대응하는 클래스가 바로 모델의 예측값이 됩니다. 다중 분류 모델은 single-label classification이므로 하나의 클래스에만 대응될 수 있습니다. 따라서 다중 분류 모델은 softmax를 통과한 값 중 가장 높은 값을 1로 남겨두고, 나머지 값들은 모두 0으로 만듭니다. 이러한 기법을 원-핫 인코딩(one-hot encoding)이라고 합니다.
2) 다중 분류 모델(multiclass classification)의 손실 함수(Loss function)
이제 오차를 정의해야 합니다. 로지스틱 회귀는 이진 교차 엔트로피(binary cross-entropy)를 사용했습니다. 다중 분류 모델은 이의 일반화 버전인 크로스 엔트로피(cross-entropy) 손실 함수를 사용합니다. 이 함수를 카테고리컬 크로스 엔트로피(categorical cross-entropy)라고도 합니다
크로스 엔트로피는 다음과 같이 생겼습니다.
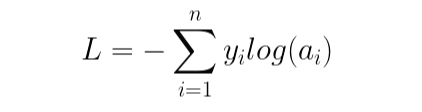
이 함수는 타깃이 1인 클래스를 제외한 모든 항이 0이 됩니다. 따라서 다음처럼도 쓸 수 있습니다.
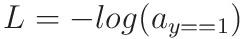
손실 함수도 준비가 되었으니 이제 다중 분류 모델에 경사 하강법을 적용해 보겠습니다.
3) 다중 분류 모델(multiclass classification)과 경사 하강법(Batch Gradient Descent)
다중 분류 모델에서 가중치와 바이어스를 업데이트하는 오류 역전파(back propagation) 알고리즘은 다음 그림과 같이 a를 구한 뒤 실행됩니다.
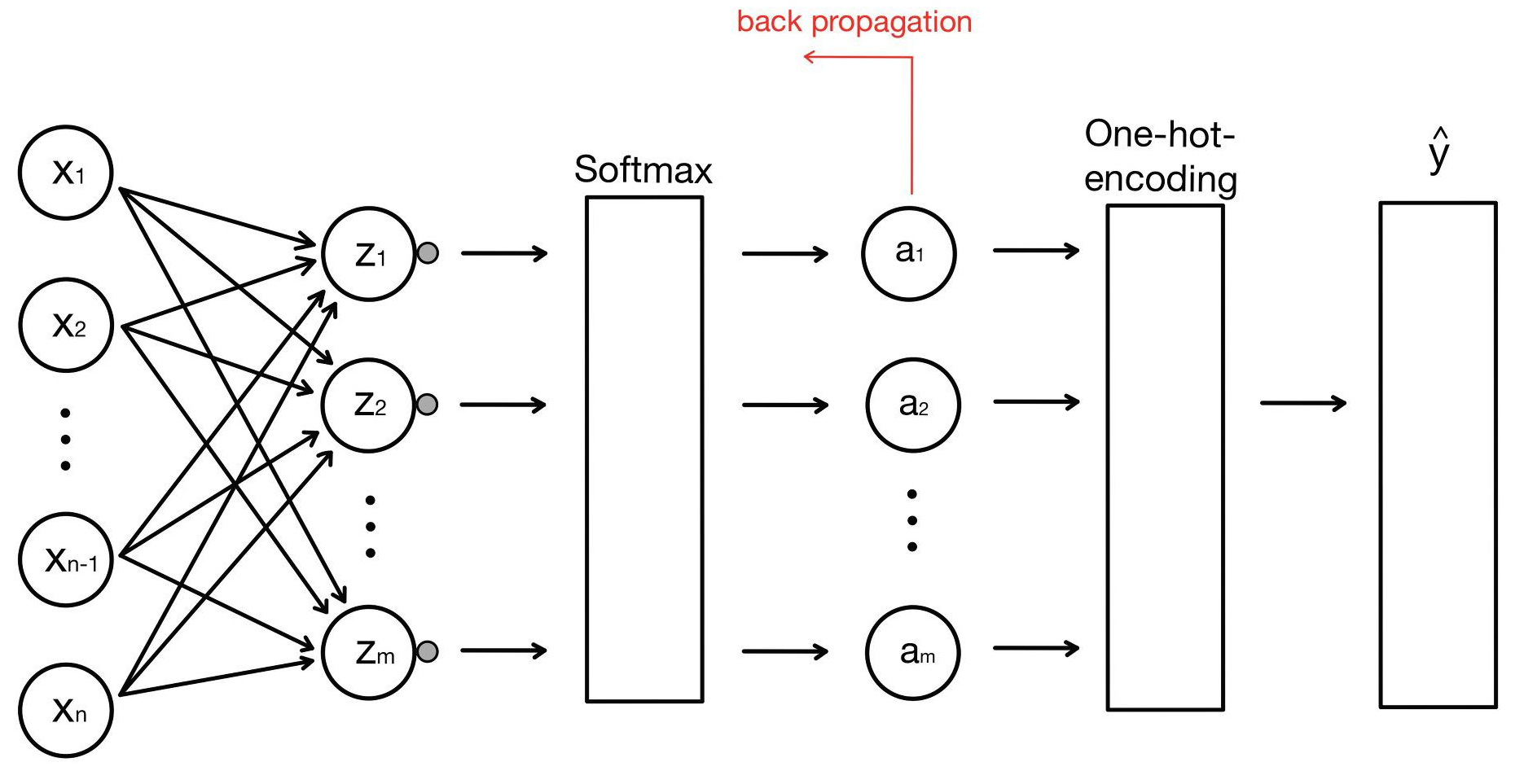
경사 하강법을 적용하여 가중치와 바이어스를 업데이트하기 위해서는 다음과 같이 가중치와 바이어스에 대한 손실 함수의 기울기를 구해야 합니다.
그전에 먼저 식을 살펴보겠습니다. 처음에 입력값의 특성에 대해 z값들이 정해졌습니다. n개의 특성값(x)이 m개의 연산값(z)에 대응이 되어야 하므로 총 m x n개의 가중치가 필요합니다. 이 m x n개의 가중치를 다음과 같이 나타냈습니다.
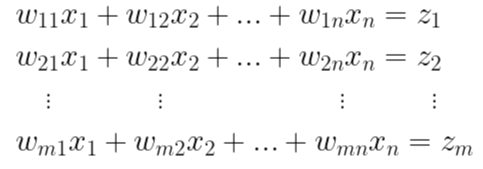
즉 z에 대한 가중치의 기울기는 다음과 같습니다.
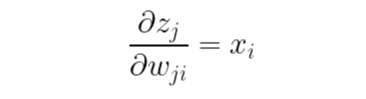
이제 a에 대한 j번째 z의 기울기를 구해보겠습니다. 한 가지 유의할 것은 m개의 a들이 전부 각각 m개의 z에 대한 함수이므로 다음과 같이 모든 편미분을 구해주어야 합니다.
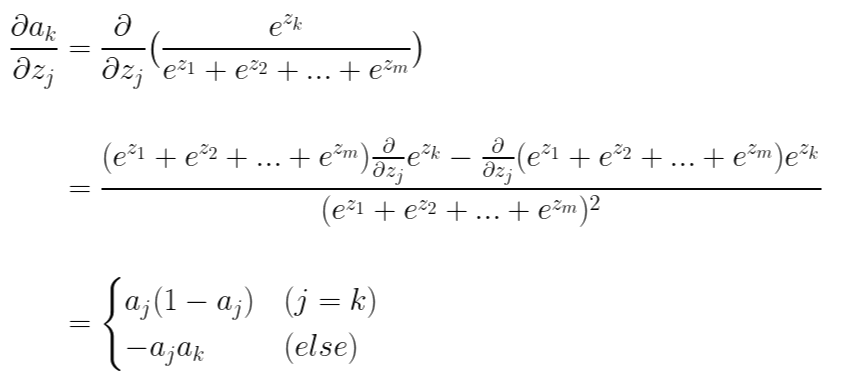
마지막으로 손실 함수 L에 대한 a의 기울기를 구해보겠습니다.
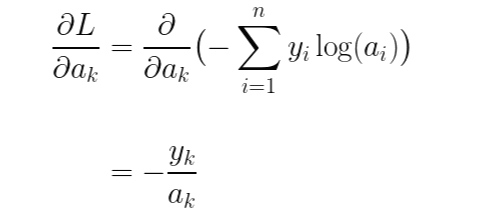
이제 연쇄 법칙(chain rule)을 이용하여 손실 함수 L에 대한 가중치의 기울기를 구해보겠습니다.
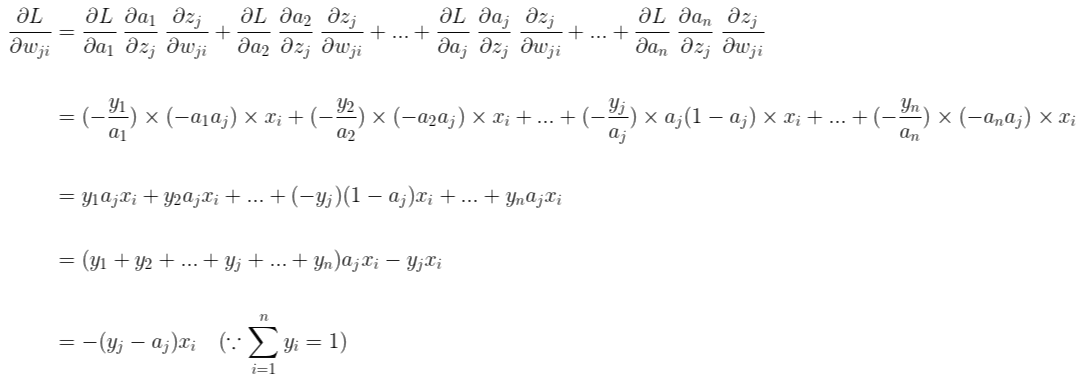
이제 경사 하강법의 방식대로 가중치를 업데이트할 차례입니다. 가중치는 다음과 같이 n x m 행렬로 나타낼 수 있습니다. (다음 포스팅의 코드의 가독성을 높이기 위해 n x m행렬로 표현했습니다.)

이 행렬 표기를 이용하여 정리를 하겠습니다.
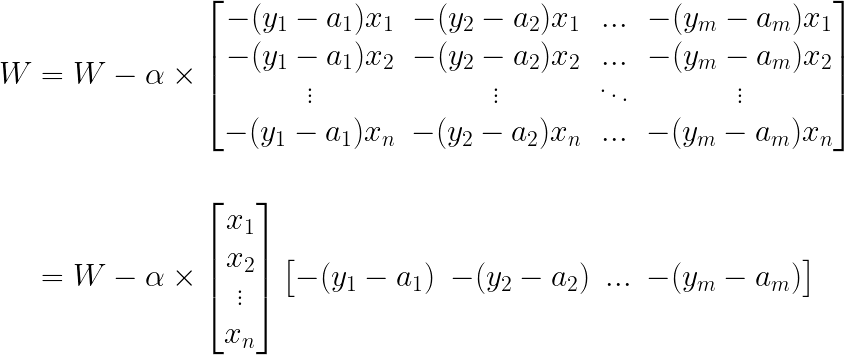
여기서 X, Y, A 행렬을 다음과 같이 정의한다면,
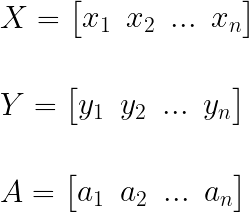
마지막으로 가중치의 업데이트는 다음과 같이 정리할 수 있습니다.
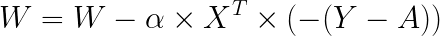
가중치가 행렬 형태이기 때문에 행렬에 대한 식으로 바뀌었을 뿐, 결국 다중 분류도 이진 분류와 똑같은 방식으로 가중치를 업데이트합니다.
지금까지 다중 분류의 구조, 손실함수와 경사하강법을 적용하는 법에 대해 정리를 했습니다. 여러개의 타깃을 갖고 있기 때문에 생기는 약간의 차이 빼고는 로지스틱 함수와 매우 비슷했습니다. 다음 포스팅에서는 지금까지 정리한 다중 분류의 정보를 바탕으로 직접 코드로 구현해보도록 하겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 데이터 세트(1) - 훈련 세트(training set), 테스트 세트(test set), 검증 세트(validation set) (0) | 2021.11.01 |
|---|---|
| 분류 (4) - 다중 분류 (Multiclass Classification) 코드 구현 (0) | 2021.10.29 |
| 분류 (2) - 위스콘신 유방암 데이터 세트(Wisconsin breast cancer dataset) (0) | 2021.10.21 |
| 분류 (1) - 이진 분류(Binary Classification)와 로지스틱 회귀(Logistic Regression) (0) | 2021.10.20 |
| 회귀 (3) - 당뇨병 환자 데이터(diabetes)와 다중 선형 회귀(Multi Regression Model) (1) | 2021.10.19 |




