머신러닝/딥러닝 공부
모델이 학습하는 방법 (2) - 경사하강법의 한계 본문
경사하강법은 머신러닝에서 모델을 주어진 데이터에 맞게 학습시킬 수 있는 좋은 방법입니다. 하지만 경사하강법은 기본적으로 기울기를 이용하여 가중치를 업데이트하기 때문에 근본적인 몇 가지 문제점을 갖습니다.
1) 많은 연산량과 컴퓨터 자원 소모
경사하강법은 데이터(입력값) 하나가 모델을 지날 때마다 모든 가중치를 한 번씩 업데이트합니다. 가중치가 적은 모델의 경우 문제가 될 것이 없으나, 만약 모델의 가중치가 매우 많다면 모든 가중치에 대해 연산을 적용하기 때문에 많은 연산량을 요구합니다. 또한 실제로 모델을 학습시킬 때 수많은 데이터를 모델에 주입시키기 때문에 상당한 연산량과 컴퓨터적 자원을 요구하게 됩니다. 모델을 평가할 때 정확도뿐만 아니라 연산량, 학습시간, 메모리 소비량 등도 평가 요소가 되기 때문에 이는 경사하강법의 치명적인 약점이라 할 수 있습니다.
이 문제를 해결하기 위해 한번의 경사하강법을 실시할 때 무작위로 하나의 가중치에 대해서만 업데이트를 하도록 하는 확률적 경사하강법(Stochastic Gradient Descent,SGD)라는 방법이 고안되었습니다.
2) Local Minima (지역 극솟값) 문제
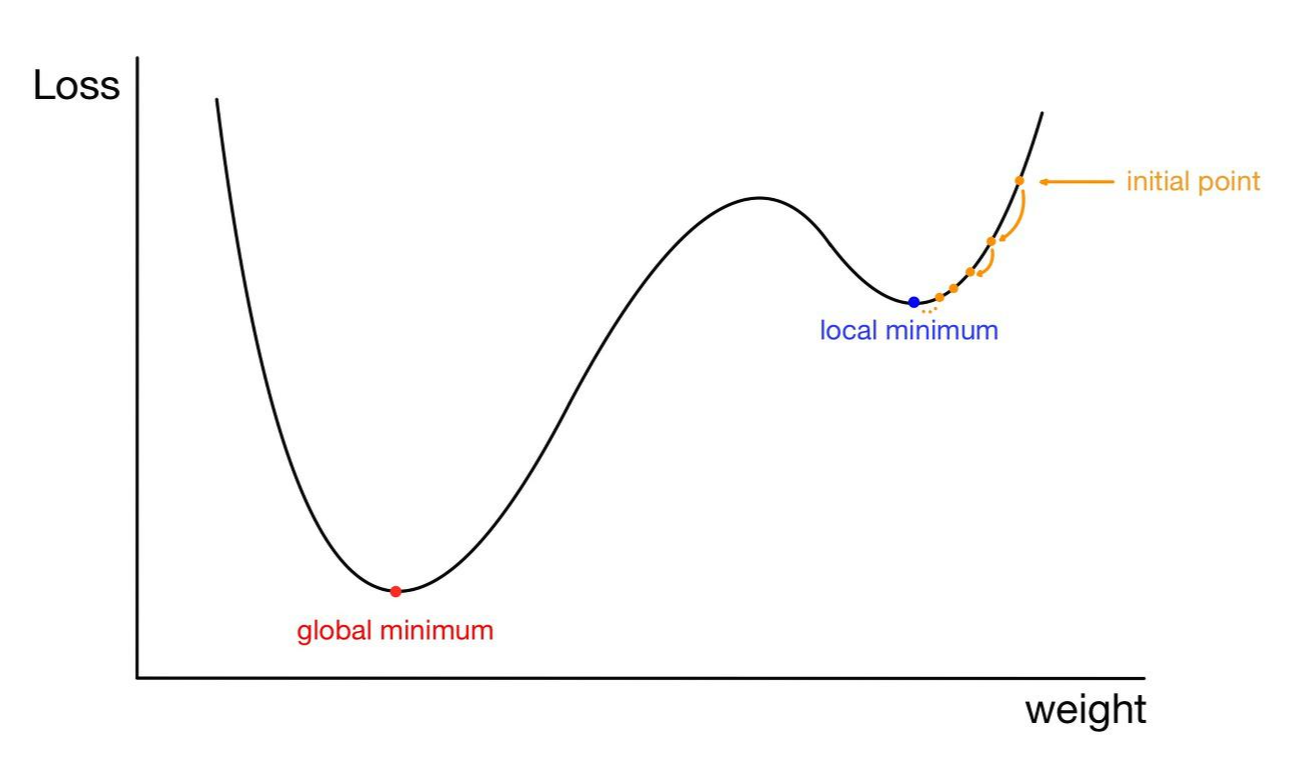
다음으로 손실함수가 지역 극솟값(local minima)들을 갖는 경우를 살펴보겠습니다. 우리가 찾아나가야 할 가중치의 값은 손실 함수가 전역 최솟값(globla minimum)을 갖는 점, 즉 그림상의 빨간 점입니다. 하지만 만약 초기 시작점이 그림상의 노란 점이라면 전역 최솟값으로 향해 다가오는 도중에 지역 극솟값에 수렴해버릴 가능성이 있습니다. 지역 극솟값에서의 손실 함수의 기울기 또한 0이므로 w가 지역 극솟값에 갇혀 더 이상 업데이트되지 못할 수 도 있다는 것입니다.
이처럼 손실함수의 전역 최솟값이 아닌 지역 극솟값으로 수렴하는 문제를 local minima문제라고 합니다.
<최근 머신러닝에서는 local minima문제가 흔히 발생하는 현상이 아니라는 의견도 있습니다. 이유는 가중치의 개수가 많아질수록 손실 함수의 critical point 대부분이 saddle point가 되고 local minimum이 될 확률이 매우 희박하기 때문입니다.
손실 함수 L이 local minimum을 가질 조건은 다음과 같습니다.

(물론 엄밀히 말해 대부분의 손실 함수가 \(C_2\)에 속하지 않겠지만 직관적인 설명을 위해 위와 같이 가정했습니다.)
위의 식에서 볼 수 있듯이 손실함수 L이 local minimum을 가지려면 모든 가중치 축에 대하여 convex 해야 합니다. 가중치가 매우 많아진다면 모든 가중치에 대해 위의 식을 만족해야 하므로 이는 고차원 상에서 흔히 일어나는 현상이 아니라는 것이죠.>
3) Plateau 현상 (고원 현상)
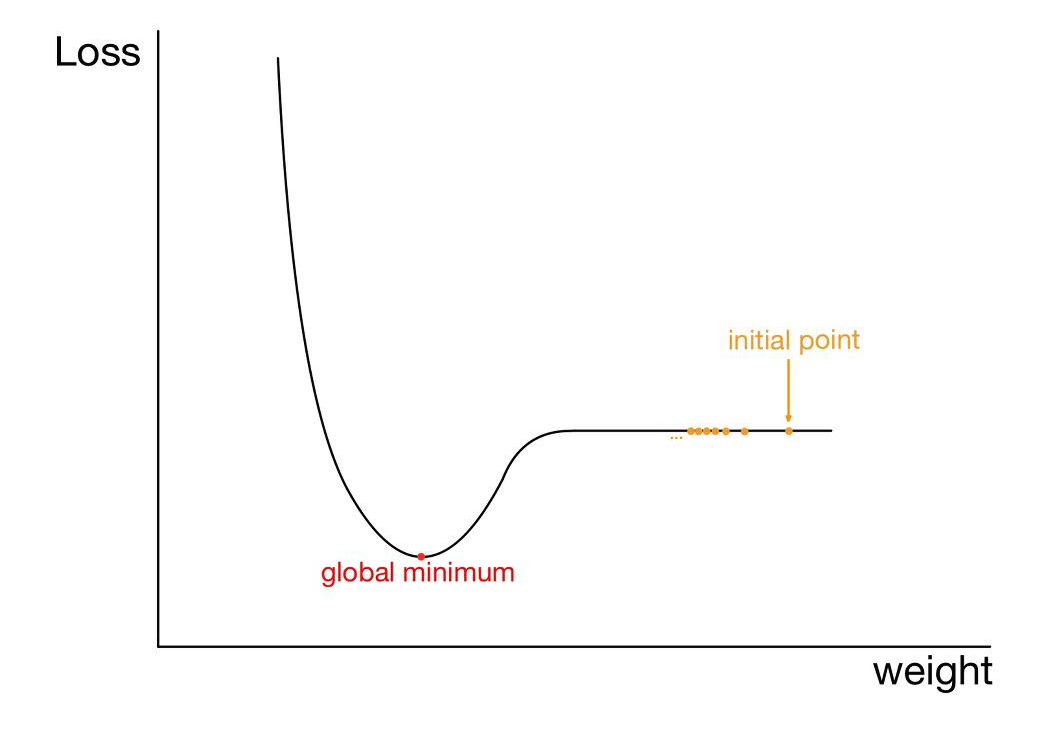
경사하강법은 기본적으로 기울기를 이용하는 방법입니다. 따라서 가중치를 기울기가 큰 지점에서는 빠르게 수렴하도록, 기울기가 작은 지점에서는 천천히 수렴하도록 해줍니다. 하지만 위의 그림과 같이 평탄한 영역에 대해서는 기울기가 0에 수렴합니다. 이런 지점에서 경사하강법을 사용하면 결국 가중치가 업데이트되지 못하고 전역 최솟값을 갖는 지점이 아닌 점에서 정지해버릴 위험이 있습니다. 이 현상은 'local minima 문제'에 비해 상대적으로 자주 발생하는 현상입니다.
4) Oscillation (진동) 문제
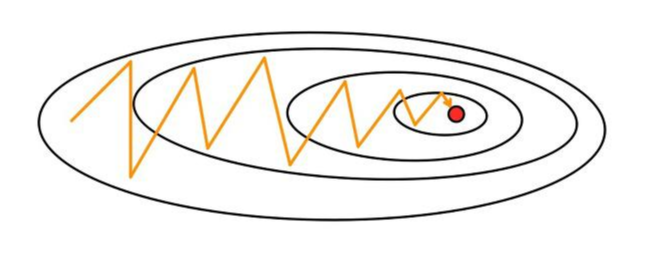
경사하강법은 현재 위치(시작 포인트)에서 최적값 방향으로 수렴하는 것이 아닌 기울기를 따라 수렴합니다. 만약 가중치들이 손실 함수에 미치는 영향이 크게 상이하다면 위의 그림과 같이 크게 진동하며 최적값에 느리게 수렴하게 됩니다. 이를 Oscillation(진동) 현상이라고 합니다.
진동폭이 크다는 것은 가중치가 불안정하게 수렴한다는 것이고, 만약 이동거리(step size)가 크다면 최적값에 수렴하지 못하고 발산해버릴 위험도 있습니다. 따라서 가중치가 업데이트될 때 진동폭을 최대한 작게 만들어주는 것 또한 옵티마이저를 설정할 때 중요한 고려사항 중 하나입니다.
경사하강법은 기울기를 이용하여 가중치를 업데이트해가며 손실 함수의 최적값을 찾아가는 방법입니다. 위의 문제들을 완화하기 위하여 경사하강법에서 보완된 여러 옵티마이저가 개발되었으나, 이들도 위의 문제들을 완벽하게 해결하지는 못합니다.
다음 포스팅에서는 경사하강법의 연산량을 개선하기 위하여 만들어진 확률적 경사하강법(SGD)와 경사하강법과 확률적 경사하강법(SGD)의 장점을 모은 미니 배치 경사하강법(mini-batch Gradient Descent)에 대해 정리하겠습니다.)
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 머신러닝 - 회귀(Regression) VS 분류(Classification) (0) | 2021.10.13 |
|---|---|
| 모델이 학습하는 방법 (3) - 확률적 경사하강법(Stochastic Gradient Descent, SGD)와 미니배치 경사하강법(mini-batch Gradient Descent) (0) | 2021.10.13 |
| 모델이 학습하는 방법 (1) - 손실함수(Loss function)와 경사하강법(Gradient Descent) (2) | 2021.10.06 |
| 머신러닝과 딥러닝의 기초 (0) | 2021.10.05 |
| 머신러닝과 딥러닝 소개 (1) | 2021.10.04 |



