머신러닝/딥러닝 공부
모델이 학습하는 방법 (1) - 손실함수(Loss function)와 경사하강법(Gradient Descent) 본문
모델이 학습하는 방법 (1) - 손실함수(Loss function)와 경사하강법(Gradient Descent)
호사린가마데라닌 2021. 10. 6. 15:441 ) 손실 함수 ( Loss function)
여태까지 다룬 내용을 한 줄로 정리해보면,
'머신러닝은 타깃과 예측값( 모델에 입력값을 넣었을 때 나오는 값, 즉 출력값)의 오차를 최소화하는 방향으로 모델의 파라미터들을 조정하여 가장 알맞은 모델을 찾아내는 것'
이라고 할 수 있습니다.
지금부터 모델이 어떤 방식으로 파라미터들을 조정하는지 정리해보겠습니다.
먼저 오차를 최소화한다고 했는데 오차는 어떤식으로 정의를 할까요?
오차를 정의하는 방법에는 여러가지가 있습니다.
- 평균 제곱 오차 (Mean Squre Error, MSE)

- 평균 제곱근 오차 (Root Mean square Error, RMSE)

- 이진 교차 엔트로피 ( Binary Cross-entropy)

- 카테고리컬 교차 엔트로피 ( Categorical Cross-entropy)

(여기서 \( y_i\)는 타깃, \( \hat{y}_i \)는 모델에 값을 대입했을 때 나오는 예측값입니다.)
이 밖에도 정말 많은 함수들이 존재합니다.
머신러닝에서는 오차를 손실(Loss) 또는 비용 (Cost), 오차(Error), 오차를 정의한 함수를 손실 함수(Loss function) 또는 비용 함수 (Cost function), 오차 함수(Error function) 이라고 합니다.
저는 손실과 손실함수라는 말이 더 익숙합니다. 따라서 앞으로 저도 '오차'와 '오차를 정의한 함수'라는 말 대신 '손실'과 '손실 함수'라는 용어를 사용하겠습니다.
머신러닝 알고리즘은 손실 함수의 값을 최소화 하는 방향으로 학습하는 것이 목적입니다.
이제 손실 함수의 값을 최소화 하는 방법을 정리해보겠습니다.
2 ) 경사하강법 ( Gradient Descent )
경사하강법(Gradient Descent)은 머신러닝 모델의 옵티마이저(Optimizer)의 한 종류입니다.
옵티마이저는 주어진 데이터에 맞게 모델 파라미터들을 최적화시켜주는 역할을 합니다. 즉, 손실 함수의 값이 최대한 작아지도록 모델 파라미터들을 조정해 줍니다.
사실 머신러닝에는 경사하강법 외에도 여러 옵티마이저가 존재합니다.

그림에서도 볼 수 있듯이 결국 다른 옵티마이저들도 경사하강법(Gradient Descent, GD)에서 새로운 개념을 추가하거나 단점을 보완해나가면서 만들어진 것이기 때문에 먼저 경사하강법에 대해 공부할 필요가 있습니다.
경사하강법은 이름에서 유추할 수 있듯이 기울기(경사, Gradient)를 이용하여 손실 함수의 값을 최소화하는 방법입니다.
한 가지 주의할 점은 우리가 조정하고자 하는 값(변수)은 가중치(weight, 이하 w)와 바이어스(bias, 이하 b)입니다. 따라서 손실 함수를 w와 b에 관한 함수로 생각을 해야 편합니다.

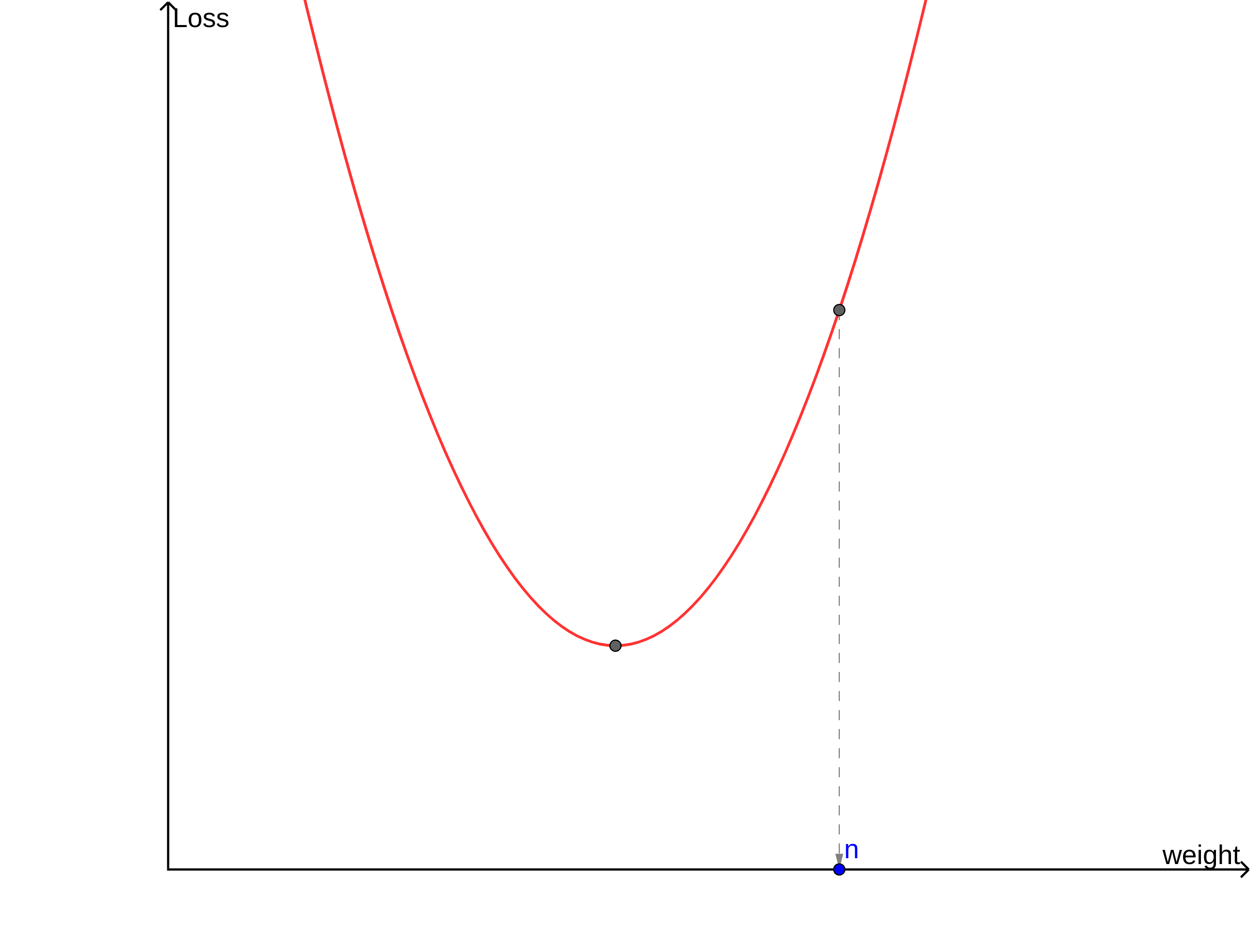
위의 그림과 같이 생긴 손실 함수가 있다고 생각해 보겠습니다. 이 손실 함수는 w=m 에서 가장 작은 값을 갖겠네요.

현재 w의 값이 n이라고 생각해보겠습니다. 손실 함수를 최솟값으로 만들어주려면 w를 오른쪽(양의 방향)으로 움직여주어야 합니다. 즉 w=w+양수 라는 식으로 w를 조정해주면 되겠군요.
이번에는 w의 값이 m보다 큰 값입니다. 마찬가지로 손실 함수를 최솟값으로 만들어주려면 w를 왼쪽(음의 방향)으로 움직여주어야 합니다. 즉 w=w+음수 라는 식으로 w를 조정해주면 됩니다.
경사하강법은 기울기를 이용하는 방법이라고 했습니다. 두 점의 기울기를 살펴보겠습니다.
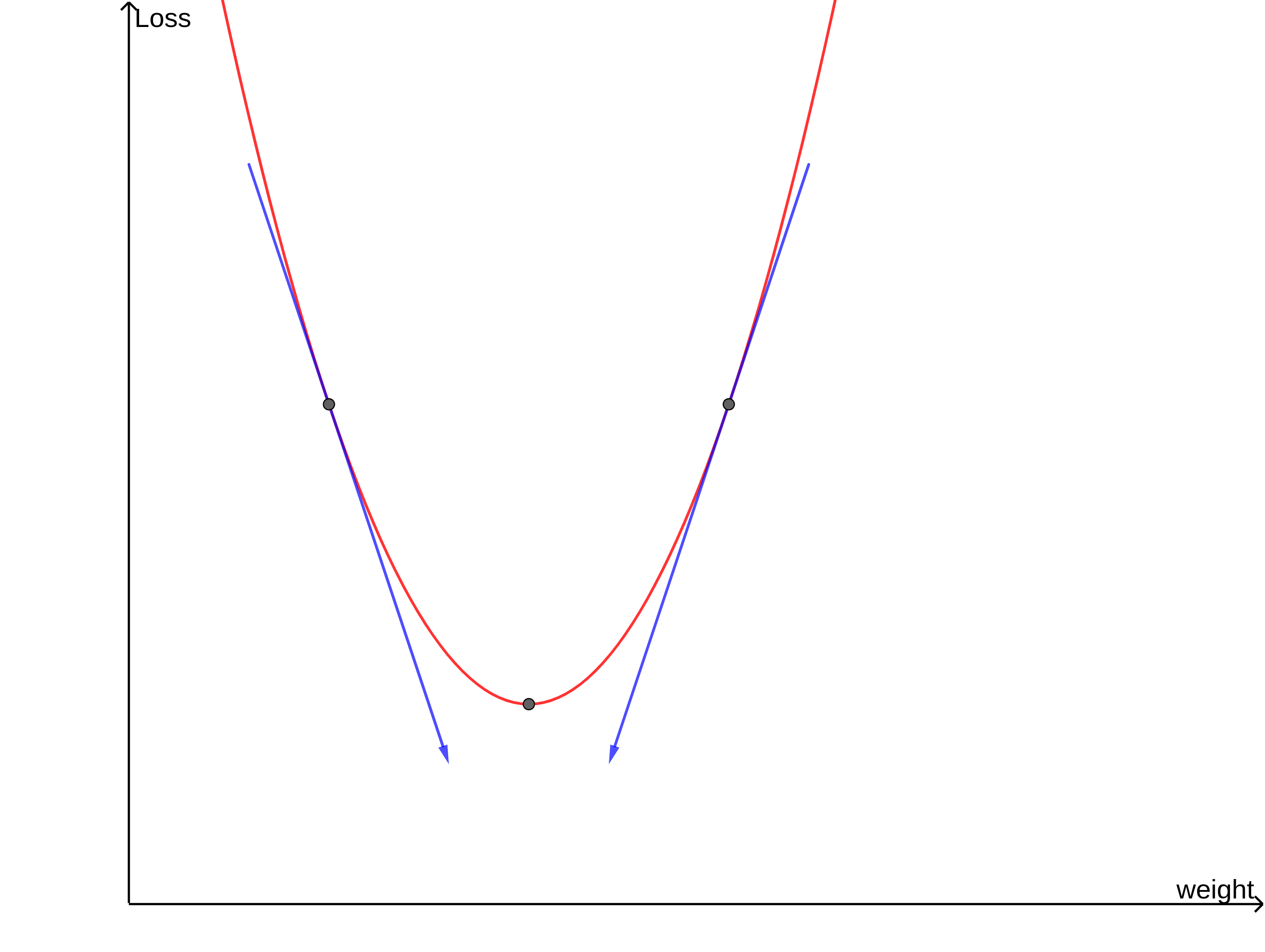
규칙이 보이네요. w값에서의 손실 함수의 미분계수가 음이라면 w를 양의 방향으로, 손실 함수의 미분계수가 양이라면 w를 음의 방향으로 이동시켜 주어야 합니다.
이제 w를 얼마만큼 이동시키는지가 관건이겠네요. 경사하강법에서는 다음과 같은 식으로 w값을 조정해줍니다.
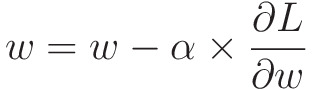
( w : weight, \( \alpha \) : learning-rate)
이런 방식을 여러번 반복하여 최종적으로 w값을 손실 함수가 최솟값을 갖도록 조정해주는 것이 바로 경사하강법입니다.
위의 방법을 사용하여 w값을 조정해주면 좋은 점이 있습니다.

그림에서 볼 수 있듯이 기울기가 크다는 것은 현재 w의 위치가 손실 함수의 극솟값을 갖는 w의 값으로부터 멀리 떨어져 있다는 것을 의미합니다. 즉 w가 이동해야 할 거리와 w에서의 미분계수의 절댓값이 비례하기 때문에 위의 식을 이용하면 w가 멀 때는 빠르게, w가 가까울 때는 천천히 수렴하도록 설정할 수 있습니다.
그렇다면 \( \alpha \)는 뭘까요?
\( \alpha \)는 학습률(Learning rate)이라는 파라미터로, w값이 움직이는 거리를 조절해주기 위해 사용합니다.
만약 w가 이동하는 거리가 너무 크다면 손실 값이 커지는 방향으로 w가 조정될 가능성이 있고, 반대로 w가 이동하는 거리가 너무 작다면 w가 적합한 값으로 수렴하는데에 너무 오랜 시간이 걸립니다.
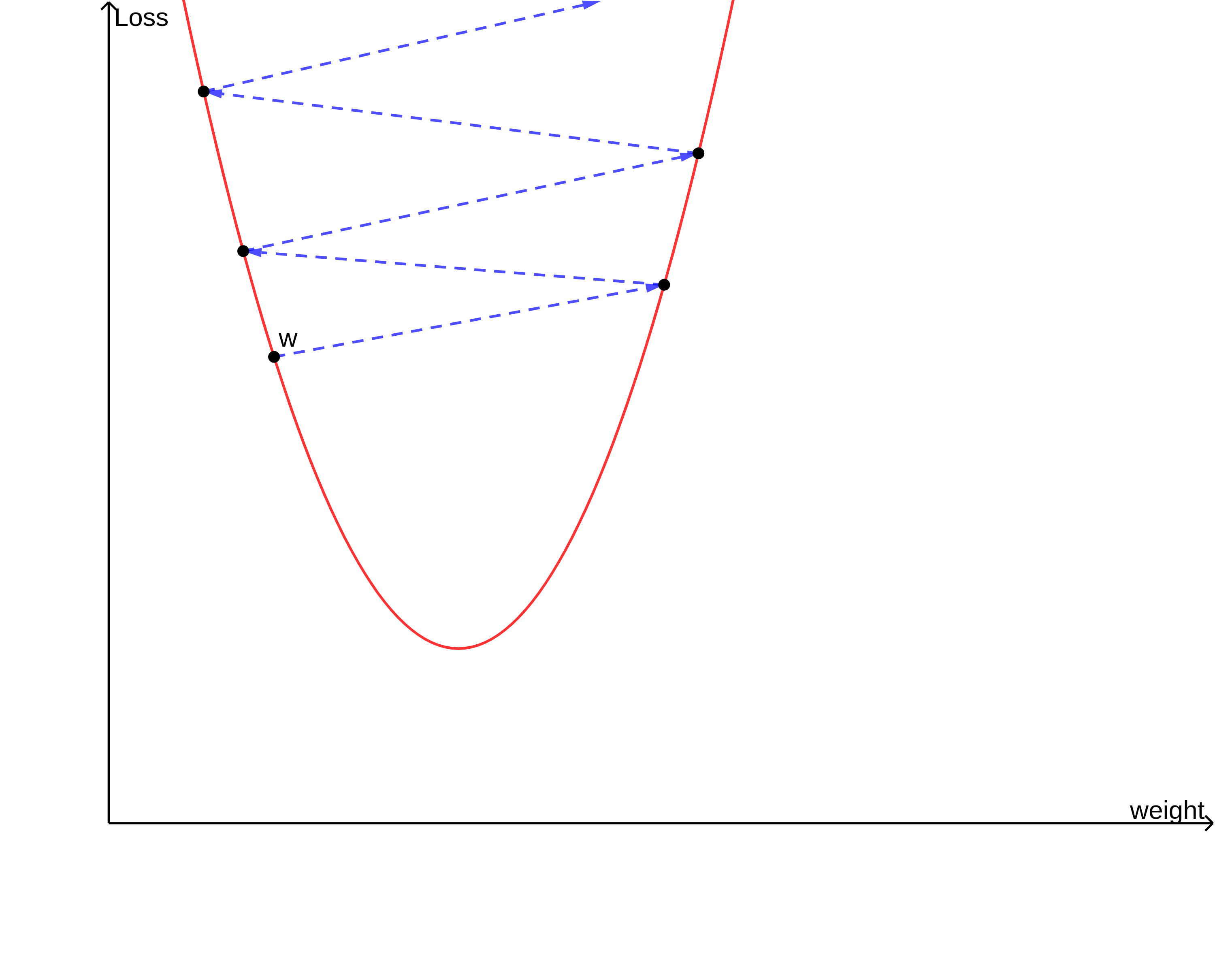
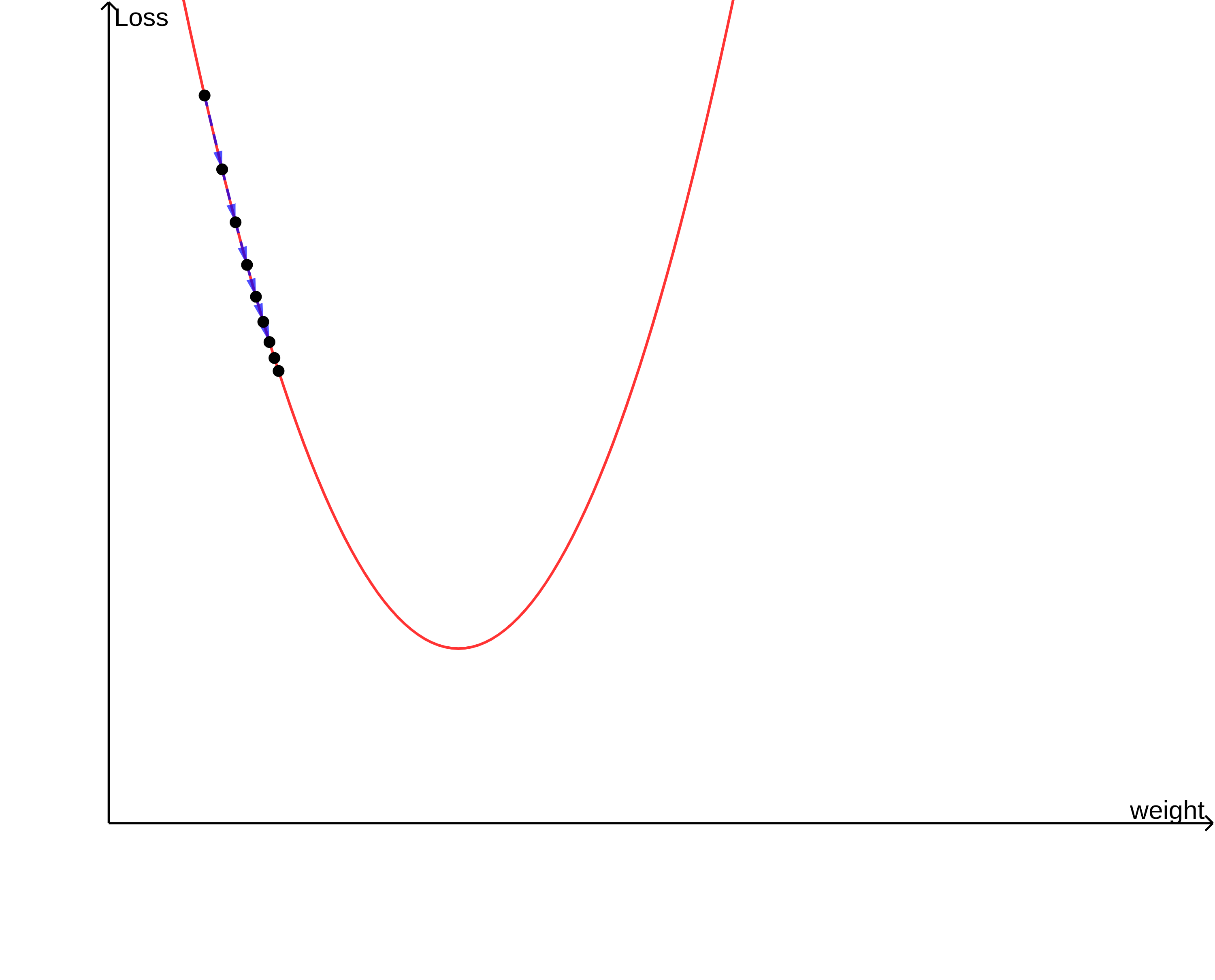
따라서 위에서 봤던 식으로 경사하강법을 상황에 맞게 적절히 조절하여 사용할 수 있겠네요.
조정해야 할 값이 하나 더 남아있죠. 옵티마이저는 가중치 외에도 바이어스를 조정합니다. 바이어스 또한 같은 방식으로 조정합니다.

한 가지 궁금한게 생기네요. 어째서 손실 함수를 그냥 미분해서 극솟값을 찾지 않는 것일까요? 그 편이 더 간단해 보이는데 말이죠.
이유는 간단합니다.
대부분의 모델은 매우 복잡하여 많은 가중치를 가지고 있습니다. 따라서 필연적으로 손실 함수 또한 매우 복잡한 형태가 됩니다. 이런 경우 많은 손실 함수들이 닫힌 형태(Closed form)가 아니거나 도함수를 구하는 계산이 복잡하고 불가능하게 됩니다.
컴퓨터에서 미분계수를 구할때는 아래의 방식으로 계산합니다.
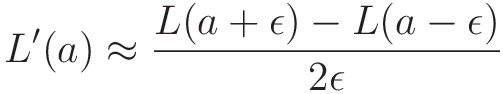
즉, 도함수를 구한뒤 값을 대입하는 것이 아니라 미분계수의 정의를 이용하여 근사하는 것이죠.
따라서 경사하강법의 방법대로 기울기를 따라 손실을 줄여나가는 방법이 컴퓨터의 자원적인 소모를 막고, 좀 더 안전한 방법이라고 할 수 있습니다.
*닫힌 형태 : 변수, 상수, 사칙연산, 초월함수(삼각함수, 지수함수, 로그함수)등을 조합하여 표현할 수 있는 형태
지금까지 손실함수와 경사하강법에 대해 정리를 해보았습니다. 다음 포스팅에서는 경사하강법이 가지는 문제점에 대해 정리를 해보겠습니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 머신러닝 - 회귀(Regression) VS 분류(Classification) (0) | 2021.10.13 |
|---|---|
| 모델이 학습하는 방법 (3) - 확률적 경사하강법(Stochastic Gradient Descent, SGD)와 미니배치 경사하강법(mini-batch Gradient Descent) (0) | 2021.10.13 |
| 모델이 학습하는 방법 (2) - 경사하강법의 한계 (1) | 2021.10.12 |
| 머신러닝과 딥러닝의 기초 (0) | 2021.10.05 |
| 머신러닝과 딥러닝 소개 (1) | 2021.10.04 |




