머신러닝/딥러닝 공부
머신러닝과 딥러닝의 기초 본문
지난번 포스팅에서 머신러닝 알고리즘의 종류 중에 지도 학습 (Supervised Learning)은 입력값(input , x)과 결괏값(target, y)을 토대로 학습을 한다고 했습니다. 그렇다면 이 학습을 하는 주체는 무엇일까요?
머신러닝에서 학습을 하는 주체를 '모델(model)'이라고 합니다. 좀 더 정확히 하자면 모델은 '입력값과 결괏값으로 학습된 머신러닝 알고리즘의 수학적 표현'입니다. 이때 학습시키는 입력값과 결괏값을 통틀어 훈련 데이터(training data)라는 표현을 사용합니다. 또한 결괏값 대신 타깃(target)이라는 용어를 더 자주 사용합니다.
저는 '학습'을 '입력값과 출력 값을 토대로 규칙을 찾아가는 것'이라고 표현을 했습니다. 그렇다면 도대체 머신러닝 모델은 어떤 규칙을 찾아가는 것일까요?
다음의 예시를 들어보겠습니다.

한 아이가 자신의 시험성적에 대하여 어머니가 화를 내실지 칭찬을 하실지 예측하는 프로그램을 작성하고자 합니다.
이 아이는 몇 번의 경험을 통해 다음과 같은 통계를 얻었습니다.
| 시험점수(x) | 어머니의 반응(y) |
| 60 점 | 화를 내심 |
| 70 점 | 화를 내심 |
| 80 점 | 칭찬을 하심 |
| 90 점 | 칭찬을 하심 |
아이는 통계를 토대로 다음의 규칙을 찾아냈습니다. (물론 여러 가지 규칙이 존재합니다.)
\( y=0.02x-0.5 \) ( y가 1 이상이면 칭찬, 1보다 작으면 화를 내심 )
위 식의 \(x\)값에 60을 넣었을 때 \(y\) 값은 0.7으로 어머니가 화를,
\(x\) 값에 80을 넣었을 때 \(y\) 값은 1.1으로 칭찬을 하십니다.
위의 표의 규칙을 잘 표현해주고 있는 식이라고 생각됩니다.
이 식을 토대로 아이가 78 점을 받으면 어머니가 칭찬을, 74점을 받으면 화를 내시는 것을 예측할 수 있습니다. 물론 데이터가 아주 적기 때문에 이 규칙은 정확도가 매우 낮을 것입니다.
사실 위의 식은 머신러닝의 종류 중 하나인 선형 회귀 모델(Linear Regression)입니다. 이 모델에 대해서는 나중에 다루도록 하려 합니다.
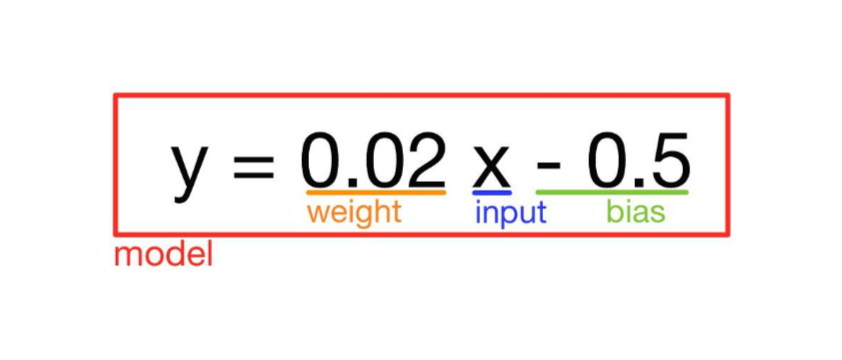
이때 위의식 \( y=0.02x-0.5 \) (y가 1 이상이면 칭찬, 1보다 작으면 화를 내심)을 모델(model),
\(x\)를 입력값(input), \(y\)를 타깃(target), 0.02와 -0.5는 각각 가중치(weight)와 바이어스(bias)라고 부릅니다.
또한 가중치와 바이어스가 모델의 출력(output)에 관여하므로 이들을 합쳐 모델 파라미터(model parameter)라고 합니다.
머신러닝의 알고리즘은 이 규칙들( 가중치와 바이어스)들을 수정해나가면서 타깃과 출력(output)의 오차를 줄이는 방식으로 모델을 조정합니다.
일반적으로 딥러닝 모델은 지도학습을 통해 모델을 구축합니다 (물론 예외도 있습니다. 생성적 적대 신경망(GAN)은 비지도 학습을 기반으로 구축한 딥러닝 모델입니다). 머신러닝과 딥러닝의 가장 큰 차이는 머신러닝은 사용자가 직접 데이터를 분석 및 가공하여 모델에 주입해야 하는 것이지만 딥러닝은 이러한 데이터의 분석(데이터의 특징을 찾아냄)을 스스로 한다는 것입니다.
이 때문에 이미 잘 가공되어 있는 데이터인 데이터베이스, 엑셀 등에 담긴 정형 데이터의 경우 머신러닝 알고리즘이 잘 처리를 하고, 데이터의 특징을 찾아내야 하는 이미지, 동영상, 음성 등의 데이터에 대해서는 딥러닝 알고리즘이 더 높은 효율을 보입니다.
다음 포스팅에서는 머신러닝에서 가중치와 바이어스를 어떤 방식으로 수정해 나가는지에 대하여 정리해보자 합니다.
'AI 공부 > Machine Learning' 카테고리의 다른 글
| 머신러닝 - 회귀(Regression) VS 분류(Classification) (0) | 2021.10.13 |
|---|---|
| 모델이 학습하는 방법 (3) - 확률적 경사하강법(Stochastic Gradient Descent, SGD)와 미니배치 경사하강법(mini-batch Gradient Descent) (0) | 2021.10.13 |
| 모델이 학습하는 방법 (2) - 경사하강법의 한계 (1) | 2021.10.12 |
| 모델이 학습하는 방법 (1) - 손실함수(Loss function)와 경사하강법(Gradient Descent) (2) | 2021.10.06 |
| 머신러닝과 딥러닝 소개 (1) | 2021.10.04 |




